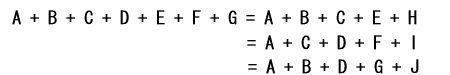
今回は、覆面算の問題です。
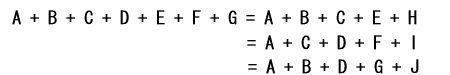
アルファベットは、A から J の 10 個使われています。 各文字に 0 から 9 までの数字を入れて、この等式を成立させるようにします。 同じ文字には、同じ数字を入れます。今回の問題は、焦点がつかみにくく少し難しく感じるかも知れません。
use strict;
my ($count, %add_5, %add_7, %henkan);
my $min = 0;
%henkan = map { $_ => $min++ } ("a" .. "j");
gen_5('', keys %henkan);
gen_7('', keys %henkan);
sub gen_5 {
my ($comb, @nums) = @_;
foreach (0 .. $#nums) {
my $work = $comb; $work .= $nums[$_];
if (length($work) == 5) {
my $n = eval(join ' + ', map { $henkan{$_} } split //, $work);
push @{$add_5{$n}}, $work;
} else {
my @tmp = @nums[$_ + 1 .. $#nums];
gen_5($work, @tmp);
}
}
}
sub gen_7 {
my ($comb, @nums) = @_;
foreach (0 .. $#nums) {
my $work = $comb; $work .= $nums[$_];
if (length($work) == 7) {
my $n = eval(join ' + ', map { $henkan{$_} } split //, $work);
push @{$add_7{$n}}, $work;
} else {
my @tmp = @nums[$_ + 1 .. $#nums];
gen_7($work, @tmp);
}
}
}
{ my %work = %add_5; %add_5 = ();
my @keys_7 = keys %add_7;
foreach my $i (keys %work) {
next if @{$work{$i}} < 3;
next unless grep /$i/, @keys_7;
push @{$add_5{$i}}, @{$work{$i}};
}
}
{ my %work = %add_7; %add_7 = ();
my @keys_5 = keys %add_5;
foreach my $i (keys %work) {
next unless grep /$i/, @keys_5;
push @{$add_7{$i}}, @{$work{$i}};
}
}
foreach (sort { $a <=> $b } keys %add_7) {
my @lst_7 = @{$add_7{$_}}; my @lst_5 = @{$add_5{$_}};
foreach my $i (@lst_7) {
foreach my $j (0 .. ($#lst_5 - 2)) {
foreach my $k (($j + 1) .. ($#lst_5 -1)) {
foreach my $l (($k + 1) .. $#lst_5) {
my $work = $i . $lst_5[$j] . $lst_5[$k] . $lst_5[$l];
next if $work !~ /^(?=.*a)(?=.*b)(?=.*c)(?=.*d)(?=.*e)(?=.*f)(?=.*g)(?=.*h)(?=.*i)(?=.*j)/;
my %hist;
$hist{$1}++ while $work =~ /(.)/g;
next if join('', sort values %hist) !~ /^1112223334$/;
next if join('', sort map { $hist{$_} } split //, $i) !~ /^2223334$/;
next if join('', sort map { $hist{$_} } split //, $lst_5[$j]) !~ /^12334$/;
next if join('', sort map { $hist{$_} } split //, $lst_5[$k]) !~ /^12334$/;
next if join('', sort map { $hist{$_} } split //, $lst_5[$l]) !~ /^12334$/;
my @sorted_num = map { $_->[0] }
sort { $a->[1] <=> $b->[1] or $a->[0] cmp $b->[0] }
map { [ $_, $hist{$_} ] } keys %hist;
my %result;
@result{'a', 'b', 'c', 'd'} = @sorted_num[9, 6, 7, 8];
foreach ($lst_5[$j], $lst_5[$k], $lst_5[$l]) {
my $tmp = $_;
if ($tmp =~ /$result{'b'}/ && $tmp =~ /$result{'c'}/) {
while ($tmp =~ /(.)/g) {
$result{'e'} = $1 if $hist{$1} == 2;
$result{'h'} = $1 if $hist{$1} == 1;
}
}
if ($tmp =~ /$result{'b'}/ && $tmp =~ /$result{'d'}/) {
while ($tmp =~ /(.)/g) {
$result{'g'} = $1 if $hist{$1} == 2;
$result{'j'} = $1 if $hist{$1} == 1;
}
}
if ($tmp =~ /$result{'c'}/ && $tmp =~ /$result{'d'}/) {
while ($tmp =~ /(.)/g) {
$result{'f'} = $1 if $hist{$1} == 2;
$result{'i'} = $1 if $hist{$1} == 1;
}
}
}
my $sum = eval(join ' + ', map { $henkan{$_} } split //, $i);
print " A B C D E F G H I J sum = $sum\n";
printf "%2d %2d %2d %2d %2d %2d %2d\n", $henkan{$result{'a'}}, $henkan{$result{'b'}},
$henkan{$result{'c'}}, $henkan{$result{'d'}}, $henkan{$result{'e'}},
$henkan{$result{'f'}}, $henkan{$result{'g'}};
printf "%2d %2d %2d %2d %2d\n", $henkan{$result{'a'}}, $henkan{$result{'b'}},
$henkan{$result{'c'}}, $henkan{$result{'e'}}, $henkan{$result{'h'}};
printf "%2d %2d %2d %2d %2d\n", $henkan{$result{'a'}}, $henkan{$result{'b'}},
$henkan{$result{'d'}}, $henkan{$result{'g'}}, $henkan{$result{'j'}};
printf "%2d %2d %2d %2d %2d\n\n", $henkan{$result{'a'}}, $henkan{$result{'c'}},
$henkan{$result{'d'}}, $henkan{$result{'f'}}, $henkan{$result{'i'}};
$count++;
}
}
}
}
}
print "解の数: $count\n";今回のプログラムの解説の前に、まず順列数と組合せ数について触れておきます。 パソコンで覆面算等のパズルを解く方法には、順列を生成して条件に合うものを見つけるというものがあります。 いわゆる虱潰しの方法ですね。この方法の弱点は、要素数が増えると実行時間が膨大になってしまうことです。 実行時間を削減する方法としては、条件に合わないものを早めに排除する " 枝刈り" というものがあります。効果的な枝刈りがある場合には、劇的に実行時間が削減できますが、 今回の問題のように枝刈りが難しいものもあります。そこで、組合せの登場という訳です。
順列の場合には順列を生成すれば後はチェックするだけというのが多いですが、 組合せの場合には、組合せを生成しただけでは正解は求められません。その先があるのです。 組合せを生かして、正解を求めるプログラムが必要になります。その点が大変といえば大変、 面白いといえば面白いところです。次に示すのは、簡単な順列生成プログラムと組合せ生成プログラムです。 その下に、私のパソコンで2つのプログラムを実行した結果を示します。
順列生成プログラム use strict; my $s = time(); my $max = 10; my $n = 10; my @work = (); search(1 .. $max); sub search { my @list = @_; foreach my $i (0 .. $#list) { push @work, $list[$i]; if (@work == $n) { print "@work\n"; } else { search(@list[0 .. $i - 1, $i + 1 .. $#list]); } pop @work; } } print time() - $s, " seconds\n"; 組合せ生成プログラム use strict; my $s = time(); my $max = 10; my $n = 7; my @work = (); search(1 .. $max); sub search { my @list = @_; foreach my $i (0 .. $#list) { push @work, $list[$i]; if (@work == $n) { print "@work\n"; } else { search(@list[$i + 1 .. $#list]); } pop @work; } } print time() - $s, " seconds\n";
| $n | 順列数 | 時間(秒) | 組合せ数 | 時間(秒) |
|---|---|---|---|---|
| 2 | 90 | - | 45 | - |
| 3 | 720 | 2 | 120 | - |
| 4 | 5040 | 12 | 210 | - |
| 5 | 30240 | 73 | 252 | - |
| 6 | 151200 | 369 | 210 | - |
| 7 | 604800 | 1476 | 120 | - |
| 8 | 1814400 | 4436 | 45 | - |
| 9 | 3628800 | 8904 | 10 | - |
| 10 | 3628800 | 8971 | 1 | - |
上の2つのプログラムは、ウリ2つに作ってあります。 違っているのは、再帰呼び出しのときの引数の配列の添字だけです。 順列を生成するプログラムでは、$n = 5 (10 の要素から 5 つの要素の順列を生成する場合) のときは "1 2 3 4 5" から "10 9 8 7 6" までのすべての順列を生成し、$n = 10 (10 の要素から 10 の要素の順列を生成する場合) のときは "1 2 3 4 5 6 7 8 9 10" から "10 9 8 7 6 5 4 3 2 1" までのすべての順列を生成します。一方組合せを生成するプログラムでは、$n = 5 (10 の要素から 5 つの要素の組合せを生成する場合) のときは "1 2 3 4 5" から "6 7 8 9 10" までのすべての組合せを生成します。
実行結果の方の時間は、元々計測方法が厳密ではありませんし、 他のプログラムも並行して動作していたので、参考程度に見て下さい。 それでも、だいたいの様子は分かると思います。尚、1秒以下の計測結果は、"-" で表示しました。実行結果の示すとおり、組合せを生成するプログラムは、 生成する組合せ数が少なく、実行時間もほとんど掛からないことが分かります。 何とか組合せを生かすプログラムを作ることができれば、短い時間で正解を出すことができます。
もう1つ組合せの利点として、あらかじめ重複解の発生を避けることができる場合があることです。 今回の問題でも、B と C と D は互いに交換可能です。これだけで、解が6つあることになります。 組合せでは、プログラムの中で "B < C < D" と指定することによって、重複解の発生を抑えられます。
今回のプログラムでは、数字を直接扱うことはしないで記号化して扱っています。 説明の最初の方では、0 から 9 の例を使いますが、最後の方で他の数字 (1 から 10 など) にも触れたいと思っています。その場合に、記号化しておくと何かと便利です。記号化には、以下のコードを使います。
my $min = 0;
%henkan = map { $_ => $min++ } ('a' .. 'j');
プログラムの最初で、ハッシュ %add_5 と %add_7 を作成します。%add_5 は、キーに5つの数字を加算したときの合計値を、値に5つの (記号化した) 数字の組合せのリストを格納します。 %add_7 も同様に7つの数字を対象に作成します。そして、作成された %add_5 から値のリストが2つ以下 (式が3つあるので) のものと、%add_7 のキーにないエントリーを削除します。同様に、%add_7 のエントリーから %add_5 のキーにないものを削除します。作成された %add_5 と %add_7 を以下に示します。
%add_5 = (
21 => [abdij, abehj, abfgj, abfhi, acdhj, acegj, acehi, acfgi, adefj, adegi, adfgh,
bcdgj, bcdhi, bcefj, bcegi, bcfgh, bdefi, bdegh, cdefh],
22 => [abeij, abfhj, abghi, acdij, acehj, acfgj, acfhi, adegj, adehi, adfgi, aefgh,
bcdhj, bcegj, bcehi, bcfgi, bdefj, bdegi, bdfgh, cdefi, cdegh],
23 => [abfij, abghj, aceij, acfhj, acghi, adehj, adfgj, adfhi, aefgi, bcdij, bcehj,
bcfgj, bcfhi, bdegj, bdehi, bdfgi, befgh, cdefj, cdegi, cdfgh],
24 => [abgij, acfij, acghj, adeij, adfhj, adghi, aefgj, aefhi, bceij, bcfhj, bcghi,
bdehj, bdfgj, bdfhi, befgi, cdegj, cdehi, cdfgi, cefgh],
25 => [abhij, acgij, adfij, adghj, aefhj, aeghi, bcfij, bcghj, bdeij, bdfhj, bdghi,
befgj, befhi, cdehj, cdfgj, cdfhi, cefgi, defgh],
26 => [achij, adgij, aefij, aeghj, afghi, bcgij, bdfij, bdghj, befhj, beghi, cdeij,
cdfhj, cdghi, cefgj, cefhi, defgi],
27 => [adhij, aegij, afghj, bchij, bdgij, befij, beghj, bfghi, cdfij, cdghj, cefhj,
ceghi, defgj, defhi],
28 => [aehij, afgij, bdhij, begij, bfghj, cdgij, cefij, ceghj, cfghi, defhj, deghi],
29 => [afhij, behij, bfgij, cdhij, cegij, cfghj, defij, deghj, dfghi],
30 => [aghij, bfhij, cehij, cfgij, degij, dfghj, efghi],
31 => [bghij, cfhij, dehij, dfgij, efghj],
32 => [cghij, dfhij, efgij],)
%add_7 = (
21 => [abcdefg],
22 => [abcdefh],
23 => [abcdefi, abcdegh],
24 => [abcdefj, abcdegi, abcdfgh],
25 => [abcdegj, abcdehi, abcdfgi, abcefgh],
26 => [abcdehj, abcdfgj, abcdfhi, abcefgi, abdefgh],
27 => [abcdeij, abcdfhj, abcdghi, abcefgj, abcefhi, abdefgi, acdefgh],
28 => [abcdfij, abcdghj, abcefhj, abceghi, abdefgj, abdefhi, acdefgi, bcdefgh],
29 => [abcdgij, abcefij, abceghj, abcfghi, abdefhj, abdeghi, acdefgj, acdefhi, bcdefgi],
30 => [abcdhij, abcegij, abcfghj, abdefij, abdeghj, abdfghi, acdefhj, acdeghi, bcdefgj, bcdefhi],
31 => [abcehij, abcfgij, abdegij, abdfghj, abefghi, acdefij, acdeghj, acdfghi, bcdefhj, bcdeghi],
32 => [abcfhij, abdehij, abdfgij, abefghj, acdegij, acdfghj, acefghi, bcdefij, bcdeghj, bcdfghi],)
次は、いよいよ正解を求める部分に移ります。正解を求めるには、合計値毎 (キーの値が同じ) に %add_7 のリストの1つと %add_5 のリストの3つの組合せを1つずつ調べていきます。 その部分の冒頭のプログラムを再掲します。
foreach (sort { $a <=> $b } keys %add_7) {
my @lst_7 = @{$add_7{$_}}; my @lst_5 = @{$add_5{$_}};
foreach my $i (@lst_7) {
foreach my $j (0 .. ($#lst_5 - 2)) {
foreach my $k (($j + 1) .. ($#lst_5 -1)) {
foreach my $l (($k + 1) .. $#lst_5) {
my $work = $i . $lst_5[$j] . $lst_5[$k] . $lst_5[$l];
foreach の5段重ねで、自分でも少し見苦しいと思っています (他にも同じようなサブルーチンやコードが並んでいるところもありますし...)。この foreach の結果、作られる $work は、式全体の数字を連結したものとなっています。$work の最初の7文字は、左側の式の数字に相当します。 その後の5文字ずつの3つのグループが、右側の式3つに相当します。こうして作られた $work を、次のような順序で正解であるか否かを判定していきます。
まず最初に次の正規表現を使って、すべての数字が使われていることを調べます。
next if $work !~ /^(?=.*a)(?=.*b)(?=.*c)(?=.*d)(?=.*e)(?=.*f)(?=.*g)(?=.*h)(?=.*i)(?=.*j)/;
この正規表現は、肯定先読みといわれるものです。$work の先頭に立って、文字列を眺め渡すというわけです。
次に、式全体の数字の数字毎の使用回数を調べて、ハッシュ %hist に格納します。
$hist{$1}++ while $work =~ /(.)/g;
ハッシュ %hist の値は、式全体の A から J のアルファベットの使用回数にマッチしていなければなりません。
式全体の使用回数がマッチしたら、次に4つの式別に使用回数を調べます。 左側の式の場合には、使用回数の組合せが "4 3 3 3 2 2 2" になっている必要があります。 右側の3つの式の場合には、それぞれが "4 3 3 2 1" になっていることを確認します。
以上の3つのチェックを通過したら、正解であるということになります。 正解が得られたら、A から J の各アルファベットに数字を割り当てる作業をします。 まず、次のコードで A, B, C, D に割り当てる数字を決定します。
my @sorted_num = map { $_->[0] }
sort { $a->[1] <=> $b->[1] or $a->[0] cmp $b->[0] }
map { [ $_, $hist{$_} ] } keys %hist;
@sorted_num の要素は、使用回数の少ない順に、 また使用回数が同じ場合には数字順に格納されます。 @sorted_num の最後の要素 $sorted_num[9] は、使用回数が 4 ですので、それを A に割り当てます。次に B, C, D には、使用回数が 3 で数字順に並んでいる @sorted_num[6, 7, 8] を割り当てます。
これで4つの数字が割り当てられましたが、まだ E, F, G, H, I, J に数字を割り当てる作業が残っています。A, B, C, D の各文字が決定したので、$work の8文字目以降の5文字ずつの3つのグループは、B と C、B と D、C と D の組合せのいずれかになっています。それを検索して、E から J までの各文字に数字を割り当てることができます。
プログラムが完成したので、実行してみましょう。正解は、以下のように 14 になります。
A B C D E F G H I J sum = 21 2 3 5 6 4 0 1 2 3 5 4 7 2 5 6 0 8 2 3 6 1 9 A B C D E F G H I J sum = 21 3 2 4 6 5 0 1 3 2 4 5 7 3 4 6 0 8 3 2 6 1 9 A B C D E F G H I J sum = 21 3 1 5 6 4 0 2 3 1 5 4 8 3 5 6 0 7 3 1 6 2 9 A B C D E F G H I J sum = 22 4 1 5 7 3 0 2 4 1 5 3 9 4 5 7 0 6 4 1 7 2 8 A B C D E F G H I J sum = 23 5 2 4 8 3 0 1 5 2 4 3 9 5 4 8 0 6 5 2 8 1 7 A B C D E F G H I J sum = 23 4 3 5 8 2 0 1 4 3 5 2 9 4 5 8 0 6 4 3 8 1 7 A B C D E F G H I J sum = 23 7 1 3 6 4 2 0 7 1 3 4 8 7 3 6 2 5 7 1 6 0 9 A B C D E F G H I J sum = 23 7 0 4 6 3 1 2 7 0 4 3 9 7 4 6 1 5 7 0 6 2 8 A B C D E F G H I J sum = 23 4 3 6 7 2 1 0 4 3 6 2 8 4 6 7 1 5 4 3 7 0 9 A B C D E F G H I J sum = 24 6 3 4 8 2 1 0 6 3 4 2 9 6 4 8 1 5 6 3 8 0 7 A B C D E F G H I J sum = 24 6 3 5 7 1 2 0 6 3 5 1 9 6 5 7 2 4 6 3 7 0 8 A B C D E F G H I J sum = 25 9 2 4 6 3 1 0 9 2 4 3 7 9 4 6 1 5 9 2 6 0 8 A B C D E F G H I J sum = 25 8 3 4 7 1 0 2 8 3 4 1 9 8 4 7 0 6 8 3 7 2 5 A B C D E F G H I J sum = 25 8 3 5 6 0 2 1 8 3 5 0 9 8 5 6 2 4 8 3 6 1 7 解の数: 14
ここまでは、始点 0 (ここから "始点 n" は、n からの連続した 10 の数字の意味で使います) について述べてきました。始点 0 以外にも正解はあります。他の始点の場合に、始点 0 の正解に始点の差を加えただけでは、左側と右側の加算している数字の数が違うため正解になりません。 今回のプログラムは、変数 $min に始点を指定することによって正解が得られるようになっています。 始点1の場合には、次の2つの正解が出力されます。
A B C D E F G H I J sum = 28 7 4 5 6 3 2 1 7 4 5 3 9 7 4 6 1 10 7 5 6 2 8 A B C D E F G H I J sum = 28 7 4 5 6 2 1 3 7 4 5 2 10 7 4 6 3 8 7 5 6 1 9 解の数: 2
他の始点では、どうでしょうか。始点 2 以上には、解はありません。 もっとも始点が 7 以上になると、そもそも式が成立しません (7 の場合、左の式の最小値が 70、右の式の最大値が 70 で1種類だけ)。正解があるのは 0 と1だけと最初は思ったのですが、実は始点を逆方向にずらす手がありました。 始点をマイナスの数値にすると、正解があります。正解があるのは、始点 -10 から -1 の範囲です。始点 -10 の正解は、次の2つです。
A B C D E F G H I J sum = -28 -7 -6 -5 -4 -2 -3 -1 -7 -6 -5 -2 -8 -7 -6 -4 -1 -10 -7 -5 -4 -3 -9 A B C D E F G H I J sum = -28 -7 -6 -5 -4 -1 -2 -3 -7 -6 -5 -1 -9 -7 -6 -4 -3 -8 -7 -5 -4 -2 -10 解の数: 2
上の始点1と始点 -10 を見比べて、始点1の正解にマイナス符号を付ければ、始点 -10 の正解になることを気付かれたでしょうか。始点 -10 の正解はそうなっていませんが、これは B, C, D を数値順に割り当てているためです。もちろん除外された重複解の中に、マイナスを取っただけのものがあります。 最後に、始点 -10 から 1 までの正解数を記して、終わりとします。
始点: -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 解の数: 2 14 32 67 98 91 91 98 67 32 14 2
(2005/08/01)