
今回は、軌跡の交差しないナイトの巡歴を取り上げます。 軌跡の交差しないナイトの巡歴では、移動元と移動先のマス目の中心を線で結びながらナイトを移動させます。 そして、その軌跡の線を交差させずに、最長手数解を求めます。 次の図は、5x5盤面での例です。

use strict;
my (%move, %stat); my @result = ("dummy");
my $m = 6; my $n = 7; ($m, $n) = ($n, $m) if $m > $n;
my @board = grep /^[1-$m][1-$n]$/, 11 .. ($m . $n);
foreach my $elm (@board) {
my $i = $elm + 1; my $j = $elm + 10;
if ($elm =~ /[^$m][^$n]/) {
$stat{"$elm:$i"} = [0, 0]; $stat{"$elm:$j"} = [0, 0];
} elsif ($elm =~ /[^$m]$n/) {
$stat{"$elm:$j"} = [0, 0];
} elsif ($elm =~ /$m[^$n]/) {
$stat{"$elm:$i"} = [0, 0];
}
}
foreach my $elm (@board) {
my ($i, $j) = split //, $elm;
@{$move{$elm}} = map { between($elm, $_) }
grep /^[1-$m][1-$n]$/, (($i - 2) . ($j - 1), ($i - 2) . ($j + 1),
($i - 1) . ($j - 2), ($i - 1) . ($j + 2),
($i + 1) . ($j - 2), ($i + 1) . ($j + 2),
($i + 2) . ($j - 1), ($i + 2) . ($j + 1));
}
sub between {
my ($a, $d) = @_; my ($b, $c, $work);
if (abs((split //, $a)[0] - (split //, $d)[0]) == 2) {
if ((split //, $a)[0] - (split //, $d)[0] == 2) {
$b = ((split //, $a)[0] - 1) . (split //, $a)[1];
if ((split //, $a)[1] - (split //, $d)[1] == 1) {
$c = (split //, $b)[0] . ((split //, $b)[1] - 1);
$work = "$b:$c:${d}z1:0";
} else {
$c = (split //, $b)[0] . ((split //, $b)[1] + 1);
$work = "$b:$c:${d}z0:1";
}
} else {
$b = ((split //, $a)[0] + 1) . (split //, $a)[1];
if ((split //, $a)[1] - (split //, $d)[1] == 1) {
$c = (split //, $b)[0] . ((split //, $b)[1] - 1);
$work = "$b:$c:${d}z1:0";
} else {
$c = (split //, $b)[0] . ((split //, $b)[1] + 1);
$work = "$b:$c:${d}z0:1";
}
}
} else {
if ((split //, $a)[0] - (split //, $d)[0] == 1) {
if ((split //, $a)[1] - (split //, $d)[1] == 2) {
$b = (split //, $a)[0] . ((split //, $a)[1] - 1);
$c = ((split //, $b)[0] - 1) . (split //, $b)[1];
} else {
$b = (split //, $a)[0] . ((split //, $a)[1] + 1);
$c = ((split //, $b)[0] - 1) . (split //, $b)[1];
}
$work = "$b:$c:${d}z0:1";
} else {
if ((split //, $a)[1] - (split //, $d)[1] == 2) {
$b = (split //, $a)[0] . ((split //, $a)[1] - 1);
$c = ((split //, $b)[0] + 1) . (split //, $b)[1];
} else {
$b = (split //, $a)[0] . ((split //, $a)[1] + 1);
$c = ((split //, $b)[0] + 1) . (split //, $b)[1];
}
$work = "$b:$c:${d}z1:0";
}
}
return $work;
}
my (@start, @end, $end);
{ my $i = 11;
my $limit = $n % 2 ? ($n + 1) / 2 : $n / 2;
my $row = $m % 2 ? ($m + 1) / 2 : $m / 2;
@start = ($i);
while (1) {
$i = $start[-1];
if ($i =~ /$limit$/) {
if ($m == $n) { $i = ((split //, $i)[0] + 1) . ((split //, $i)[0] + 1); }
else { $i = ((split //, $i)[0] + 1) . '1'; } }
else { $i++; }
push @start, $i;
last if $i =~ /$row$limit/;
}
@start = @start[0 .. ($#start - 1)] if $m % 2 and $n % 2;
foreach my $elm (@start) {
my $i = (split //, $elm)[0] - 1; my $j = (split //, $elm)[1] - 1;
push @end, $elm, (split //, $elm)[0] . ($n - $j),
($m - $i) . (split //, $elm)[1], ($m - $i) . ($n - $j);
push @end, (split //, $elm)[1] . (split //, $elm)[0], ($n - $j) . (split //, $elm)[0],
(split //, $elm)[1] . ($m - $i), ($n - $j) . ($m - $i) if $m == $n and $elm !~ /(.)\1/;
}
}
foreach my $start (@start) {
$end = join ':', @end;
$end = substr $end, 0, index($end, $start) + 2;
my @save = @{$move{$start}};
if ($m == $n and $start =~ /(.)\1/) {
my (@work, $chk);
foreach my $elm (@{$move{$start}}) {
my $chk = (split /z/, $elm)[0];
$chk = join ':', map { (split //)[1] . (split //)[0] } split /:/, $chk;
push @work, $elm unless grep /$chk/, @work;
}
@{$move{$start}} = @work;
}
if ($n % 2 and substr($start, 1, 1) == ($n + 1) / 2) {
my (@work, $chk);
foreach my $elm (@{$move{$start}}) {
my $chk = (split /z/, $elm)[0];
$chk = join ':', map { (split //)[0] . ($n + 1 - (split //)[1]) } split /:/, $chk;
push @work, $elm unless grep /$chk/, @work;
}
@{$move{$start}} = @work;
}
if ($m % 2 and substr($start, 0, 1) == ($m + 1) / 2) {
my (@work, $chk);
foreach my $elm (@{$move{$start}}) {
my $chk = (split /z/, $elm)[0];
$chk = join ':', map { ($m + 1 - (split //)[0]) . (split //)[1] } split /:/, $chk;
push @work, $elm unless grep /$chk/, @work;
}
@{$move{$start}} = @work;
}
search($start);
@{$move{$start}} = @save;
}
sub search {
my $route = shift;
my $c_p = substr($route, -2);
my $flag = 0;
foreach (@{$move{$c_p}}) {
my ($tmpa, $tmpb) = split /z/;
my $n_p = substr($tmpa, -2);
next if $route =~ /\b$n_p\b/;
my ($b, $c, undef) = split(/:/, $tmpa);
my @pattern = split /:/, $tmpb;
my $side1 = $c_p < $b ? "$c_p:$b" : "$b:$c_p";
next if $stat{$side1}->[$pattern[0]];
my $side2 = $b < $c ? "$b:$c" : "$c:$b";
next if $stat{$side2}->[0] or $stat{$side2}->[1];
my $side3 = $c < $n_p ? "$c:$n_p" : "$n_p:$c";
next if $stat{$side3}->[$pattern[1]];
$stat{$side1}->[$pattern[0]] = 1;
@{$stat{$side2}} = (1, 1);
$stat{$side3}->[$pattern[1]] = 1;
$flag = 1;
search(join(':', $route, $n_p));
$stat{$side1}->[$pattern[0]] = 0;
@{$stat{$side2}} = (0, 0);
$stat{$side3}->[$pattern[1]] = 0;
}
unless ($flag) {
return if $end =~ /$c_p/;
if (length($result[$#result]) < length($route)) {
@result = ($route);
} elsif (length($result[$#result]) == length($route)) {
push @result, $route;
}
}
}
print join("\n", @result), "\n";
通常のナイトの巡歴は、以前に取り上げています。 マス目の番号の付け方の付け方は、通常のナイトの巡歴と同じです。
my $m = 5; my $n = 5; ($m, $n) = ($n, $m) if $m > $n; my @board = grep /^[1-$m][1-$n]$/, 11 .. ($m . $n);
| 11 | 12 | 13 | 14 | 15 |
| 21 | 22 | 23 | 24 | 25 |
| 31 | 32 | 33 | 34 | 35 |
| 41 | 42 | 43 | 44 | 45 |
| 51 | 52 | 53 | 54 | 55 |
軌跡の交差しないナイトの巡歴では、プログラムの中でどのように軌跡を表現するかが難題です。 分からないときには、観察して検討してみるのが一番です。下の例は、ナイトを 22 から 34 に移動しています。
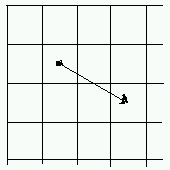
上の図を見ながら検討すると、次のようなことが分かります。
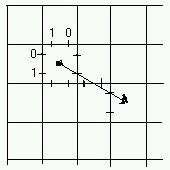
以上のような軌跡の線の性質を頭に置きながら考えているうちに、隣り合う四角形 (マス目) が共有する辺に2つのチェックポイントを設けることを思いつきました。上の図にチェックポイントを書き込むと、 次のようになります。図の右側のコードが、チェックポイントを生成します。
 |
foreach my $elm (@board) {
my $i = $elm + 1; my $j = $elm + 10;
if ($elm =~ /[^$m][^$n]/) { # 右側と下側の両方にマス目が存在する
$stat{"$elm:$i"} = [0, 0]; $stat{"$elm:$j"} = [0, 0];
} elsif ($elm =~ /[^$m]$n/) { # 下側のみマス目が存在する
$stat{"$elm:$j"} = [0, 0];
} elsif ($elm =~ /$m[^$n]/) { # 右側のみマス目が存在する
$stat{"$elm:$i"} = [0, 0];
}
} |
右側のコードによって生成されるハッシュ %stat は、キーに (外周を除く) すべての辺を保持し、値に2つのチェックポイントが設定されます。チェックポイントを設ける位置は、両端から 1/4 の地点です。チェックポイントは、0 で初期化しておきます。無名配列の2つの値のうち、 最初の値は横の辺では右側を指し、縦の辺では上側を指します (図の 0, 1 は、無名配列のインデックスの数字)。
例に挙げた 22 から 34 にナイトを移動する場合は、
の4つのチェックを通過したらナイトを移動できます。 ナイトを移動したら、それぞれのチェックポイントに1をセットしておきます。 これで、軌跡の線を引きながらナイトを移動できるはずというのが、私の目論見です。
通常のナイトの巡歴では、22 => [14, 34, 41, 43] のように単純なマス目の番号の移動先リストを使いました。今回のパズルでは、22 => [23:13:14z0:1, 23:33:34z1:0, 32:31:41z1:0, 32:33:43z0:1] のような移動先リストになります。: と z は、単なる区切り文字です。23:13:14z0:1 は、22 から 23, 13 を通過して 14 に至り、1番目の辺のチェックポイントは上側で、 3番目の辺のチェックポイントは下側になるという、意味になります (尚、2番目の辺は2つ一緒に扱うので必要ありません)。この移動リストを生成しているのが、サブルーチン between になります。
| 12 | 14 | |||
| 21 | 25 | |||
| 33 | ||||
| 41 | 45 | |||
| 52 | 54 |
sub between {
my ($a, $d) = @_; my ($b, $c, $work);
if (abs((split //, $a)[0] - (split //, $d)[0]) == 2) { # 12, 14, 52, 54
if ((split //, $a)[0] - (split //, $d)[0] == 2) { # 12, 14
$b = ((split //, $a)[0] - 1) . (split //, $a)[1];
if ((split //, $a)[1] - (split //, $d)[1] == 1) { # 12
$c = (split //, $b)[0] . ((split //, $b)[1] - 1);
$work = "$b:$c:${d}z1:0";
} else { # 14
$c = (split //, $b)[0] . ((split //, $b)[1] + 1);
$work = "$b:$c:${d}z0:1";
}
} else { # 52, 54
$b = ((split //, $a)[0] + 1) . (split //, $a)[1];
if ((split //, $a)[1] - (split //, $d)[1] == 1) { # 52
$c = (split //, $b)[0] . ((split //, $b)[1] - 1);
$work = "$b:$c:${d}z1:0";
} else { # 54
$c = (split //, $b)[0] . ((split //, $b)[1] + 1);
$work = "$b:$c:${d}z0:1";
}
}
} else { # 21, 25, 41, 45
if ((split //, $a)[0] - (split //, $d)[0] == 1) { # 21, 25
if ((split //, $a)[1] - (split //, $d)[1] == 2) { # 21
$b = (split //, $a)[0] . ((split //, $a)[1] - 1);
$c = ((split //, $b)[0] - 1) . (split //, $b)[1];
} else { # 25
$b = (split //, $a)[0] . ((split //, $a)[1] + 1);
$c = ((split //, $b)[0] - 1) . (split //, $b)[1];
}
$work = "$b:$c:${d}z0:1";
} else { # 41, 45
if ((split //, $a)[1] - (split //, $d)[1] == 2) { # 41
$b = (split //, $a)[0] . ((split //, $a)[1] - 1);
$c = ((split //, $b)[0] + 1) . (split //, $b)[1];
} else { # 45
$b = (split //, $a)[0] . ((split //, $a)[1] + 1);
$c = ((split //, $b)[0] + 1) . (split //, $b)[1];
}
$work = "$b:$c:${d}z1:0";
}
}
return $work;
}ナイトの移動先は、最大で8カ所になります。サブルーチン between は、8カ所の移動先を箇条書きしただけのものです。ナイトが 33 にある場合 (図) の移動先がどこに該当するかを、付記しておきました。それにしても、split を書き過ぎました。もう少し考えるべきだったかも知れません。
軌跡の交差しないナイトの巡歴では、通常のナイトの巡歴とは違いすべてのマス目を 訪れることはできません。サブルーチン search を使って深さ優先探索を行いますが、 1つの探索が行き詰まったときに手数を数える必要があります。その部分のコードは、次のようになります。
sub search {
・・・
my $flag = 0; # フラグをセット
foreach (@{$move{$c_p}}) {
・・・
$flag = 1; # 次の移動先がある場合に1をセット
search(join(':', $route, $n_p));
・・・
}
unless ($flag) { # 次の移動先がない
・・・
if (length($result[$#result]) < length($route)) {
@result = ($route);
} elsif (length($result[$#result]) == length($route)) {
push @result, $route;
}
}
}
サブルーチン search の最初の方で、変数 $flag を 0 にセットしておきます。 そして、次の移動先がある場合には、$flag に1をセットして search を再帰呼び出しします。 呼び出しから帰ってきたときも、$flag は1のままですので手数を数えません。 探索に行き詰まって次の移動先がない場合には、$flag が 0 のままになっている (unless ($flag)) ので手数を数えます。
最長手数解は、配列 @result に格納します。探索の途中では、その時点での (1つまたは複数の) 最長手数解が入っています。1つの探索が行き詰まったときの手数は3つのケースがあり、 そのときの処理は次のようになります。
これですべての探索が終了すると、@result には最長手数解だけが残ることになります。
このパズルでは、すべての経路を探索しなければなりません。 探索時間の関係もあり探索開始位置を絞りたかったのですが、最長手数解が 11 にあるとは限りません。例えば、6 x 6 盤面では 12 からの探索に最長手数解があります。また、最長手数解が周辺からの探索にあるとは限りません。 6 x 7 盤面の探索では、23 の開始位置に最長手数解の1つがあります。 そこで、対称位置にあるマス目を除くすべてのマス目を探索開始位置にしました。図の青色のマス目は、5 x 5 と 5 x 6 盤面での探索開始位置です。
|
|
縦と横のマス目の数が同じ正方形盤面では、重複解となる対称位置が多くなります。 5 x 5 盤面での 12 の対称位置は、14, 21, 25, 41, 45, 52, 54 となります。12 から探索すれば、他の位置からの探索は重複解となり探索しなくてもよいことになります。それに比べて 5 x 6 の盤面では、12 と 21 は対称位置にはなりません。12 の対称位置は 15, 52, 55 となり、21 の対称位置は 26, 41, 46 となって、別に探索することになります。
図の 5 x 5 盤面の 33 が探索開始位置に含まれていないのを、疑問に思われるかも知れません。 実は、重複解にならない終了位置がないのです。33 の探索を開始されるまでには、11, 12, 13, 22, 23 の探索が終了しています。33 から探索して、探索済みのいずれかが終了位置の場合には、 逆順の重複解ということになります。探索済み以外の位置が終了位置となった場合も、 探索済み位置の対称位置となりますので、結局は重複解となります。5 x 5 盤面の 33 は、対称位置のないマス目です。7 x 7 の 44 マス目も対称位置のないマス目で、探索の必要がありません。
図の 5 x 6 盤面では、33 の位置が探索開始位置に含まれています。これは、終了位置が 34 になるときのみ重複解にはなりません。それ以外の位置が終了位置の場合は、すべて重複解です。6 x 6 盤面での 33 からの探索は、終了位置が 34, 43, 44 のときに重複解とはなりません。
次のコードで、探索開始位置を生成しています。
my (@start, @end, $end);
{ my $i = 11;
my $limit = $n % 2 ? ($n + 1) / 2 : $n / 2;
my $row = $m % 2 ? ($m + 1) / 2 : $m / 2;
@start = ($i);
while (1) {
$i = $start[-1];
if ($i =~ /$limit$/) {
if ($m == $n) { $i = ((split //, $i)[0] + 1) . ((split //, $i)[0] + 1); }
else { $i = ((split //, $i)[0] + 1) . '1'; } }
else { $i++; }
push @start, $i;
last if $i =~ /$row$limit/;
}
@start = @start[0 .. ($#start - 1)] if $m % 2 and $n % 2;
foreach my $elm (@start) {
my $i = (split //, $elm)[0] - 1; my $j = (split //, $elm)[1] - 1;
push @end, $elm, (split //, $elm)[0] . ($n - $j),
($m - $i) . (split //, $elm)[1], ($m - $i) . ($n - $j);
push @end, (split //, $elm)[1] . (split //, $elm)[0], ($n - $j) . (split //, $elm)[0],
(split //, $elm)[1] . ($m - $i), ($n - $j) . ($m - $i) if $m == $n and $elm !~ /(.)\1/;
}
}
foreach my $start (@start) {
$end = join ':', @end;
$end = substr $end, 0, index($end, $start) + 2;
・・・
search($start);
}
重複解の問題は、実に厄介です。まずは探索開始位置が複数あることから生ずる特有の 重複解から説明します。この重複解をチェックするために、探索開始位置を生成する上のコード中で、配列 @end を作成しておきます。@end は、開始位置とその対称位置をすべて格納しています。5 x 5 と 5 x 6 盤面では、次のような内容になります。
5 x 5: 11 15 51 55 12 14 52 54 21 41 25 45 13 13 53 53 31 31 35 35
22 24 42 44 23 23 43 43 32 32 34 34
5 x 6: 11 16 51 56 12 15 52 55 13 14 53 54 21 26 41 46
22 25 42 45 23 24 43 44 31 36 31 36 32 35 32 35 33 34 33 34
太字で示してあるのが開始位置で、その後ろが対称位置になります (中には重複しているものもありますが、あるかないかが重要ですので実用上問題ありません)。search で開始位置を指定して探索を始める際に、開始位置より前の配列の要素を連結して $end を作成します (実際の $end は、開始位置も含めています。11 からの探索のときに、$end が空文字列にならないようにしただけです)。13 から探索する場合の $end は、次のようになります。
5 x 5: 11:15:51:55:12:14:52:54:21:41:25:45:13 5 x 6: 11:16:51:56:12:15:52:55:13
search サブルーチンの中では、次のコードでチェックをしています。$c_p は、探索終了位置です。$c_p が $end に含まれている場合は、重複解として除外されることになります。
return if $end =~ /$c_p/;
次は、対称解の問題です。 対称解は、探索開始位置や盤面によって違いますが、3つあります。
ここでは、7 x 7 盤面の開始位置 33 のケースを検討してみることにします。
|
@{$move{33}} @{$move{33}}
23:22:12z1:0 23:22:12z1:0
23:24:14z0:1 23:24:14z0:1
32:22:21z0:1 ===>
34:24:25z0:1 34:24:25z0:1
32:42:41z1:0
34:44:45z1:0 34:44:45z1:0
43:42:52z1:0
43:44:54z0:1 |
33 の位置は、図に緑と赤で示した8カ所の移動場所があります。11 から 77 の対角線マス目を軸としてみた場合、12 と 21、14 と 41、25 と 52、45 と 54 は対称的な位置関係になります。 対称解の除外は、対称関係にある2カ所の内の片方だけを探索すればできることになります。@{$move{33}} に入って 33 の移動リストを、次のコードで減らします。
foreach my $start (@start) {
・・・
my @save = @{$move{$satrt}};
if ($m == $n and $start =~ /(.)\1/) {
my (@work, $chk);
foreach my $elm (@{$move{$start}}) {
my $chk = (split /z/, $elm)[0];
$chk = join ':', map { (split //)[1] . (split //)[0] } split /:/, $chk;
push @work, $elm unless grep /$chk/, @work;
}
@{$move{$start}} = @work;
}
・・・
search($start);
@{$move{$start}} = @save;
}
これで @{$move{33}} の移動リストは、図に青で示してある4カ所になります。 経路の探索は新しい移動リストを元に行われるので、対称解は発生しません。 他の2つの対称解も、同様な方法で除外します。
今回のパズルは、複数の開始位置から探索することやすべての経路を探索するために、 それなりの実行時間がかかります。5 x 5 の盤面から始めて、横のマス目と縦のマス目の数を交互に1つずつ増やしながら、8 x 8 盤面まで行いました。5 x 6, 6 x 6, 7 x 8 盤面では、最長手数解が1つだけです。
5 x 5: 最長手数 10 11:23:15:34:55:43:24:32:53:41:22 12:24:45:53:34:22:43:51:32:11:23 12:24:45:53:34:42:23:11:32:51:43 12:31:23:15:34:55:43:24:32:53:41 12:31:23:44:32:51:43:55:34:13:25
5 x 6: 最長手数 14 12:24:16:35:23:11:32:51:43:22:34:46:54:33:45
6 x 6: 最長手数 17, 6seconds 12:31:23:15:34:26:45:66:54:35:43:24:32:51:63:44:52:33
6 x 7: 最長手数 21, 101seconds 12:31:43:22:34:13:25:17:36:24:45:33:54:42:61:53:65:44:56:35:47:66 21:42:61:53:32:11:23:15:34:22:43:35:56:44:63:55:67:46:25:17:36:57 23:35:14:22:34:46:25:17:36:57:45:33:21:42:61:53:32:44:56:64:43:55
6 x 7 盤面の軌跡は、3つとも図形としての面白さや美しさがあります。 開始位置と終了位置が対称的な位置関係になり、180 度回転すると図形全体が重なります。 鑑賞に値する軌跡と言えるでしょう。最後の解を図にしましたので、ご覧下さい。
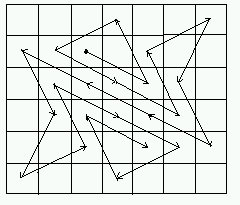
7 x 7: 最長手順 24, 733seconds (12分13秒) 12:31:23:42:34:13:25:17:36:24:45:37:56:77:65:46:54:75:63:71:52:64:43:51:32 12:31:23:44:32:51:43:64:52:71:63:75:54:46:65:77:56:37:45:24:36:17:25:13:34 12:31:23:44:32:51:43:64:52:71:63:75:54:46:65:77:56:37:45:26:34:13:25:17:36 12:31:43:22:34:13:25:17:36:24:45:33:54:42:61:53:72:64:76:57:65:44:56:35:47 12:31:43:22:34:13:25:17:36:24:45:33:54:42:61:73:52:64:76:57:65:44:56:35:47 12:31:43:22:34:13:25:17:36:24:45:33:54:42:63:51:72:64:76:57:65:44:56:35:47 13:25:17:36:24:12:33:21:42:61:73:52:64:76:57:65:53:32:44:23:35:47:55:34:46 13:25:17:36:24:12:33:21:42:63:51:72:64:76:57:65:53:32:44:23:35:47:55:34:46 14:33:25:44:36:15:27:46:67:75:56:64:45:53:34:42:23:11:32:51:43:62:54:73:65 22:34:13:25:17:36:24:45:33:21:42:61:73:52:64:43:55:74:66:47:35:56:44:32:53 22:34:13:25:17:36:24:45:33:21:42:63:51:72:64:43:55:74:66:47:35:56:44:32:53 33:45:24:36:17:25:13:34:22:41:53:32:44:56:35:47:66:54:75:63:71:52:64:43:55 33:45:57:36:17:25:46:34:15:23:11:32:44:56:77:65:73:54:42:63:71:52:31:43:55
7 x 8: 最長手順 30, 20,572seconds (5時間42分52秒) 14:33:25:44:36:15:27:48:56:37:45:53:34:42:23:11:32:51:43:62:54:46:65:57:78:66:74:55:63:71:52
8 x 8: 最長手順 35, 226,297seconds (62時間51分37秒) 22:34:55:43:64:52:73:81:62:41:53:32:11:23:15:36:24:45:66:54:75:63:84:76:88:67:46:58:37:18:26:47:35:56:77:65 23:11:32:53:41:62:81:73:52:64:43:22:34:13:25:17:38:26:47:55:36:24:45:33:54:75:63:84:76:88:67:48:56:77:65:44 23:11:32:53:41:62:81:73:52:64:43:22:34:13:25:37:16:28:47:55:36:24:45:33:54:75:63:84:76:88:67:48:56:77:65:44 34:22:43:64:52:73:81:62:41:53:32:11:23:15:36:24:45:33:54:75:63:84:76:88:67:46:58:37:18:26:47:35:56:77:65:44
最近、新しいパソコンを購入しました。プロサイド(株)の静音を売りにしたミニタワーの Mecole eco140 というモデルで、CPU は Celeron M, 1.4GHz、メモリ 1GB です。今まで使っていたのが 800MHz の CPU ですので、2倍まではなりませんがかなり速くなりました。今回の実行時間は、新しいパソコンで計測したものです。
(2006/06/15)