経路の探索

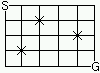
今回は、経路の探索について考えてみることにしましょう。経路の探索では、格子状の経路を始点 (下図の S: Start) から終点 (G: Goal) までの経路数を数えます。経路の進み方は、遠回りすることは許されず、右または下方向のみに移動してゴールを目指すことになります。なお、左の図のようにすべての地点を通ることができるのであれば、経路数は計算によって簡単に求めることもできますが、右の図のように任意の地点が通れないとなると、途端に難しくなり手に負えなくなってしまうこともあります。

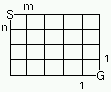
手始めに、始点から経路をたどって、終点に着いたらカウントアップするというプログラムです。それぞれの分岐点は、上の右側に示しているように２つの数字をコロン (:) でつないだものを使います (このようにしておけば、２桁以上の大きさの経路でも対応できます)。現在の地点から次の地点に進むには、コロンの前後の数字にそれぞれ１プラスするだけで済みます (現在地点が 1:1 の場合、次の地点は 2:1 と 1:2)。

プログラム１
use strict;
use warnings;
my ($m, $n) = (5, 6);
my ($start, $goal, $route, $call) = ("1:1", "$m:$n", 0, 0);
my %ng = ();   # 右図: ('2:3' => 0, '3:5' => 0, '4:2' => 0)
search($start);

sub search {
  ++$call;
  my $pos = shift;
  if ($pos eq $goal) {
    ++$route;
  } else {
    my ($i, $j) = split /:/, $pos;
    my $next_1 = ($i + 1) . ":$j";
    my $next_2 = "$i:" . ($j + 1);
    search($next_1) if $i < $m and !exists($ng{$next_1});
    search($next_2) if $j < $n and !exists($ng{$next_2});
  }
}

print "$route, $call\n";

プログラム１は単にゴール地点でカウントアップするだけでしたが、別の考え方でプログラムを作ることもできます。ここで参考になるのがフィボナッチ数列のアルゴリズムで、経路の探索にも応用できます。n 番目のフィボナッチ数を求めるには、n - 1 番目の数値と n - 2 番目の数値を加算します。下記のフィボナッチの式を再帰型サブルーチンを使ってコード化すれば、プログラムはできあがります。

経路の探索の場合、ある地点の経路数は次に進むことができる地点の経路数を合計した数値となります。例えば、スタート地点 (1:1) の経路数は、右隣の地点 (1:2) の経路数が m で、直下の地点 (2:1) の経路数が n であるとすれば m + n で算出することができます。このことは、探索上のどの地点にも当てはまるので、再帰型サブルーチンを適用することができます。なお、ゴール (5:6) に隣接する２つの地点 (4:6 と 5:5) の経路数は１であることは自明ですので、ゴール地点で１を返せば再帰型サブルーチンを停止させることができます。

フィボナッチ数列と異なるのは、必ずしも次に進める地点が２つ存在するとは限らない点です。フィボナッチ数列では直前の２つの値は必ず存在しますが、経路の探索では通過することができない地点や右隣がない地点 (x:6) や直下がない地点 (5:x) があります。その場合には、0 を加算することで対応するようにしています。

プログラム２
use strict;
use warnings;
my ($m, $n) = (5, 6);
my ($start, $goal, $call) = ("1:1", "$m:$n", 0);
my %ng = ();   # 右図: ('2:3' => 0, '3:5' => 0, '4:2' => 0)
print search($start), " $call\n";

sub search {
  ++$call;
  my $pos = shift();
  my ($i, $j) = split /:/, $pos;
  return 1 if $pos eq $goal;
  my $next_1 = ($i + 1) . ":$j";
  my $next_2 = "$i:" . ($j + 1);
  return ($i == $m || exists $ng{$next_1} ? 0 : search($next_1)) +
         ($j == $n || exists $ng{$next_2} ? 0 : search($next_2));
}

プログラム１とプログラム２では考え方は違いますが、ほぼ同じように機能します。経路数が同じになるのはむろんですが、呼び出されるサブルーチンの回数も同じになります。5 x 5 のサイズから 15 x 15 までのサイズでの経路数とサブルーチンの呼出数は、以下のようになります。なお、12 x 12 以上のサイズについては、私のパソコンで計測した秒数を付記してあります。

	経路数	呼出数		経路数	呼出数		経路数	呼出数	秒数
5x5:	70	251	8x9:	6,435	24,309	12x12:	705,432	2,704,155	5.4
5x6:	126	461	9x9:	12,870	48,619	12x13:	1,352,078	5,200,299	10.3
6x6:	252	923	9x10:	24,310	92,377	13x13:	2,704,156	10,400,599	20.6
6x7:	462	1,715	10x10:	48,620	184,755	13x14:	5,200,300	20,058,299	40.1
7x7:	924	3,431	10x11:	92,378	352,715	14x14:	10,400,600	40,116,599	83.0
7x8:	1,716	6,434	11x11:	184,756	705,431	14x15:	20,058,300	77,558,759	164.7
8x8:	3,432	12,869	11x12:	352,716	1,352,077	15x15:	40,116,600	155,117,519	307.5

再帰型サブルーチンの欠点としてコード中で複数の再帰呼び出しをすると、呼出数が非常に多くなってしまうことです。１つの呼び出しであれば呼出数も予測できますが、複数の呼び出しでは実際に数えてみてその多さに驚くことになります。サブルーチンの呼出数は、サイズが大きくなるにつれて、地点数に比例するだけではなく加速度的に多くなっていきます。１地点あたりの呼出数でみてみると、5 x 5: 10.04 (251 ÷ 25), 6 x 6: 25.64, 7 x 7: 70.02, ... 13 x 13: 61542.01, 14 x 14: 204676.53, 15 x 15: 689411.20 のようになっています。

もう少し呼出数を解析するために、5 x 6 のサイズにおける各地点別の呼出数を調べてみましょう。プログラムでは、各地点おける呼出数は $call を %call (キーに各地点) に変更すれば簡単に数えることができます。

１番上の行の各地点と１番左の列の各地点は１回の呼び出しですが、それ以外の地点は複数回の呼び出しが行われていることがわかります。ゴール地点の呼び出しが最大で、コール地点に近い地点ほど多く呼び出されています。戻り値が違う場合はダメですが、戻り値が同じ場合は最初の呼び出し時に戻り値を記憶しておき、２回目からはその値を活用できそうです。プログラム２を改造したのが、次のプログラム３になります。

プログラム３
use strict;
use warnings;
my ($m, $n) = (5, 6);
my ($start, $goal, $call) = ("1:1", "$m:$n", 0);
my %route = ($goal => 1); # 右図: ('2:3' => 0, '3:5' => 0, '4:2' => 0, $goal => 1)

print search($start), ", $call\n";

sub search {
  ++$call;
  my $pos = shift();
  my ($i, $j) = split /:/, $pos;
  my $next_1 = ($i + 1) . ":$j";
  my $next_2 = "$i:" . ($j + 1);
  my $count;
  if ($i < $m and $j < $n) {
    $count = (exists($route{$next_1}) ? $route{$next_1} : search($next_1)) +
             (exists($route{$next_2}) ? $route{$next_2} : search($next_2));
  } elsif ($i < $m) {
    $count = exists($route{$next_1}) ? $route{$next_1} : search($next_1);
  } else {
    $count =exists($route{$next_2}) ? $route{$next_2} : search($next_2);
  }
  $route{$pos} = $count unless exists $route{$pos};
  return $count;
}

各地点の経路数を記憶しておくために、ハッシュ %route を使います。%route の初期化では、ゴール地点を値１に設定し、また通過することができない地点があれば 0 を指定しておきます。プログラム３でのサブルーチンの呼出数は、ゴール地点を除く各地点１回なので 5 x 6 のサイズでは 29 回になります。プログラム１と２は 461 回でしたので、大幅に減少しました。また、プログラム１と２で 15 x 15 のサイズを探索すると 155,117, 519 (１億５千万強) 回のサブルーチンの呼び出しがあって 307 秒かかりましたが、プログラム３では呼出数が 224 回で、時間も 0.01 秒未満で実行することができます。これほど効率面で差があるプログラム例も珍しいと思います。

15 x 15 のサイズで 0.01 秒未満で実行できるので、いつもの例にもれず、サイズを拡大しながら不都合がでるまで実行してみることにします。縦と横をそれぞれ１ずつ増やしながら実行してみると、28 x 28 のサイズで経路数が整数の範囲を越えて指数表記になってしまいました。また、51 x 51 のサイズでは、"Deep recursion ..." という再帰呼出回数に関するウォーニングが出てしまいました。なお、51 x 51 のサイズでも、0.03 秒未満の時間で実行することができました。

最後のプログラムとして、再帰呼び出しを使わない方法を考えてみました。各地点の経路数の表を眺めていて、プログラムのヒントを見つけることができました。以下の表は、5 x 5 のサイズで 2:3, 3:5, 4:2 が通過できない地点 (表では x で示してある) である場合の、各地点の経路数です。

表を見ると、１番下の行または右端の列をコード化するのは簡単であることがわかります。例えば、１番下の行にはその下に行がないので、基本的には右隣の経路数を受け継ぎます。したがって、ゴールの左隣から始めて先頭に向かってを割り当てることになります。１番下の行に通過できない地点がないとすると、経路数はすべて１になります。通過できない地点があるとすれば、その地点から先頭までが 0 になります。

１番下の行に経路数が割り当ててあれば、それを基に下から２行目を割り当てることができます。右端の地点は下の行から経路数を受け継ぐだけですが、それ以外の地点は右隣の地点と直下の地点の経路数を加算します (通過できる地点の場合)。なお、通過できない地点の場合は、単に 0 を入れておきます。0 を入れておけば、その地点を参照する地点は、通常の加算処理を行うことができます。なお、下から３行目以降最終行 (上から１行目) までは、下から２行目と同様の方法で割り当てることができます。

プログラム４
use strict;
use warnings;
my ($m, $n) = (5, 6);
print "${m}x$n: ";
my %ng = (); # 右図: map { $_->[0], { $_->[1] => 1 } } ([2, 3], [3, 5], [4, 2]);
my %route = (even => ['dummy', map { [$_] } (0) x ($n - 1), 1],    # 偶数行を格納
             odd  => ['dummy', map { [$_] } (0) x ($n - 1), 1]);   # 奇数行を格納

foreach my $i (reverse 1 .. $m) {
  my ($this, $below) = $i % 2 ? ('odd', 'even') : ('even', 'odd');
  foreach my $j (reverse 1 .. $n) {
    if (exists $ng{$i}->{$j}) {   # 通過できない地点
      @{$route{$this}->[$j]} = 0;
    } elsif ($j == $n) {          # 右端の地点
      @{$route{$this}->[$j]} = @{$route{$below}->[$j]};
    } else {                      # 上記以外
      @{$route{$this}->[$j]} = add($route{$this}->[$j+1], $route{$below}->[$j]);
    }
  }
}

my $result = reverse(join '', @{$route{odd}->[1]});
print length($result), "\n";
$result =~ s/\d{50}(?=\d)/$&\n/g;
print "$result\n";

sub add {
  my ($ref_1, $ref_2) = sort { $#$b <=> $#$a } @_;
  my @num_1 = @$ref_1; my @num_2 = @$ref_2;
  return @num_1 if @num_2 == 1 and $num_2[0] == 0;
  return @num_2 if @num_1 == 1 and $num_1[0] == 0;
  my @answer;
  foreach my $i (0 .. $#num_1) {
    if ($i <= $#num_2) { $answer[$i] += $num_1[$i] + $num_2[$i]; }
    else { $answer[$i] += $num_1[$i]; }
    if ($answer[$i] >= 10) {
      $answer[$i+1] = 1;
      $answer[$i] -= 10;
    }
  }
  return @answer;
}

プログラムに特に難しい点はありませんが、行単位で経路数を格納しておくハッシュ %route について説明しておきます。ハッシュ %route には、奇数行用と偶数行用の２行分のデータを保存します。5 x 6 サイズの場合、%route は次のように初期化してあります。

初期化してある理由は、下から１行目を下から２行目以降と同様に処理できるようにするためです。ループの１回目に特別な処理が必要な場合、ループに入る前に処理する、ループ中で判断のための条件分岐入れる、等の方法もあります。どれがいいという問題ではなく、コードが簡潔に記述できるため採用しました。

無名配列の先頭の要素は、1 から $n そのままでアクセスできるようにダミーとして入れてあります。添字 1 から $n までの要素にその行の経路数を入れますが、その経路数は１桁単位に分解して無名配列に格納します。２つの地点の経路数を加算して次の地点の経路数を計算する場合、add サブルーチンに２つの無名配列を渡し、渡された add サブルーチンは１桁単位の加算をすることで大きな桁数の加算も処理できるようになっています。

プログラムが開始されると、まず最初に下から１行めと２行目が %route に格納されます。奇数の行数サイズでは下から１行目が odd に２行目が even に格納され、偶数の行数サイズでは下から１行目が even に２行目が odd に格納されます。先の表の例は 5 x 6 (奇数行数) のサイズですので、２行格納すると以下のようになります。

下から１行目が odd に、下から２行目が even に格納されています。次の下から３行目は odd に格納し、保存してあった下から１行目は捨てられます。ある行の経路数を計算するにはすぐ下の行のみが必要なので、それ以前の行を捨ててしまっても差し支えありません。下から4行目以降も同様に処理していくと、最終行 (上から１行目) は必ず odd に格納されます。その 'dummy' を除く最初の要素にスタート地点の経路数が格納されることになります。

以下に、サイズ 100 x 100, 500 x 500, 1000 x 1000 のときの実行結果を示します。最初の行が「サイズ、桁数、秒数」で、次の行から経路数を表示してあります。なお、経路数は 50 桁ごとに折り返してあります。