数字1個: a, b, c, d 連続した数字2つの和: a+b, b+c, c+d, d+a 連続した数字3つの和: a+b+c, b+c+d, c+d+a, d+a+b 連続した数字4つの和: a+b+c+d
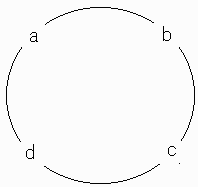
今回は、円上に数字を配置する問題です。下の図は、円上に4つの数字 a, b, c, d が配置してあります。a, b, c, d は異なる数字で、それぞれの位置を起点として、1 つから個数未満の 時計回りに連続した数字の和を求めます。飛び飛びの a+c などは駄目です。 それ以外に、すべての数字の和はどこを起点としても同じなので1つだけにします。
 |
数字1個: a, b, c, d 連続した数字2つの和: a+b, b+c, c+d, d+a 連続した数字3つの和: a+b+c, b+c+d, c+d+a, d+a+b 連続した数字4つの和: a+b+c+d |
値の数は、全部で 13 個になります。この 13 個の値が、1から 13 になるような数字 a, b, c, d の組合せを見つけて下さいというのが、今回の問題です。 円上の数字の個数は、5個でも6個でも解がありますが、7個では解がなく8個では解があります。
use strict;
my $n = 7;
my $max = $n * ($n -1) + 1;
my @overlap;
comb($max - 3, 3, $n - 2, 2);
sub comb {
my ($num, $min, $div, @comb) = @_;
my $limit;
{ my $i = eval(join '+', 1, @comb) + 1;
my $j = int(($num - eval(join '+', 0 .. ($div - 1))) / $div);
$limit = $i < $j ? $i : $j;
}
foreach my $i ($min .. $limit) {
my @list = @comb;
push @list, $i;
if ($div == 2) {
push @list, $num - $i;
@overlap = map { $_, $max - $_ } @list[1 .. $#list];
foreach my $j (0 .. ($#list - 1)) {
if ($list[1] == 3 and $list[2] == 4) {
next if $j == 0 or $j == 1;
my $chk = 1 + $list[$j];
next if grep /^$chk$/, @overlap;
} elsif ($list[1] == 3) {
next if $j == 0;
last if $j == 2;
} else {
last if $j == 1;
}
foreach my $k (($j + 1) .. $#list) {
my $ret = check($list[$k], 1, $list[$j]);
next unless $ret;
my @save = @overlap;
push @overlap, @$ret, 1 + $list[$j];
my @work = grep { ! /^$list[$j]$/ and ! /^$list[$k]$/ } @list;
perm([$list[$k], 1, $list[$j]], \@work);
@overlap = @save;
}
}
} else {
comb( $num - $i, $i + 1, $div - 1, @list);
}
}
}
sub perm {
my @order = @{shift()};
my @rest = @{shift()};
if (@rest == 1) {
my @list = ($rest[0], @order);
my @work,
my $i = $#list - 1;
my $j = 0;
while ($i--) {
foreach (($j ? $j : 1) .. ($#list - 2)) {
my $add = eval(join('+', @list[0 .. $_]));
return if grep /^$add$/, @overlap, @work;
push @work, $add;
}
@list = @list[$#list, 0 .. $#list - 1];
$j++;
}
push @order, $rest[0];
print join('_', @order[1 .. $#order], $order[0]), "\n";
} else {
foreach my $i (0 .. $#rest) {
my $ret = check($rest[$i], reverse @order);
next unless $ret;
my @save = @overlap;
push @overlap, @$ret;
push @order, $rest[$i];
my @tmp = @rest[0 .. $i - 1, $i + 1 ..$#rest];
perm(\@order, \@tmp);
@overlap = @save;
pop @order;
}
}
}
sub check {
my @list = @_;
my @work;
foreach (1 .. $#list) {
last if $#list == $n - 2 and $_ == $#list;
my $add = eval(join '+', @list[0 .. $_]);
return 0 if grep /^$add$/, @overlap;
push @work, $add;
}
return \@work;
}今回のパズルの解法は、だいたいのところ次のようになります。
円上に配置した N 個の整数の合計値を求める
円上に N 個の整数を配置した場合に、その合計値は、(整数1個の場合を含む) 加算式
の数によって求めることができます。整数1個が N 個、整数2個の和が N 個、・・・、整数 (N - 1) 個の和が N
個、それにすべての整数の和が1個になります。それぞれの加算式に、
1から連続した整数が割り当てられることになります。
my $max = ($n - 1) * $n + 1;
合計値を N 個の整数に分割する
合計値が得られたら、その合計値になる整数 N 個の組み合わせを生成します。
分割した N 個の整数を円上に並べる
円上に並べる場合には、順列を生成しながら条件に合うか調べていきます。
まず最初に、整数を N 個に分割する一般的なプログラムを作ってみました。 ごく簡単で短いプログラムで易しいので、すぐにわかると思います。 そのプログラムは、次のようなものです。
use strict;
my $m = 13; my $n = 4;
comb($m, 1, $n, ());
sub comb {
my ($num, $min, $div, @comb) = @_;
# my $limit = int($num / $div);
my $limit = int(($num - eval(join '+', 0 .. ($div - 1))) / $div);
foreach my $i ($min .. $limit) {
my @work = @comb;
push @work, $i;
if ($div == 2) {
push @work, $num - $i;
print "@work\n";
} else {
# comb($num - $i, $i, $div - 1, @work);
comb($num - $i, $i + 1, $div - 1, @work);
}
}
}このプログラムでは、分割する整数を $m で、分割数を $n で指定します。comb の4つの引数は、それぞれ、未分割の合計値、分割する際の最小値、分割数、分割済みのリスト (起動のときは空リスト) となります。コメントアウトしてある2行は、同じ数字が重複してもいい分割をする場合に使います。 同じ数字が重複可の分割をするときは、コメントを外して、次の行をコメントアウトします。 このプログラムを実行すると、次のような出力が得られます。
同じ数字が重複可の分割 同じ数字が重複不可の分割 1 1 1 10 1 2 3 7 1 1 2 9 1 2 4 6 1 1 3 8 1 3 4 5 1 1 4 7 1 1 5 6 1 2 2 8 1 2 3 7 1 2 4 6 1 2 5 5 1 3 3 6 1 3 4 5 1 4 4 4 2 2 2 7 2 2 3 6 2 2 4 5 2 3 3 5 2 3 4 4 3 3 3 4
同じ数字が重複可の分割は、同じ数字が重複不可の分割に比較して生成数が非常に多くなります。 今回のパズルに当てはめると、次のような生成数になります。なお、最後の行は、今回のパズルでの生成数です。
$m,$n 13,4 21,5 31,6 43,7 57,8 73,9 91,10 111,11 133,12
同じ数字重複可 18 101 612 4,011 27,493 195,666 1,431,884 10,718,685 -
同じ数字重複不可 3 10 35 131 525 2,194 9,418 41,373 185,425
今回のパズル 2 6 21 77 304 1,257 5,356 23,392 104,311
今回のパズルでは異なる数字を配置しますので、同じ数字が含まれない分割になります。 同じ数字が含まれない分割を使いますが、パズルの性質上さらに生成数を少なくすることができます。第1に、1と 2 は加算によって得られず必ず含まれることになりますので、この2つの数字を含まない分割は除外することができます。 そこで、comb の呼び出しは、次のように変更することができます。
comb($m - 3, 3, $n - 2, (1, 2)); # 実際のプログラムでは $m は $max
第2に、次に分割する整数を、すでに分割済みの整数の和に1加えたものまでに制限できます。 少しわかりにくい表現なので、例を挙げて説明しましょう。comp の呼び出しのときは、すでに 1 と 2 は分割済みです。次の分割する整数は、3 から $limit までとなります。$limit の式は、次のようになっています。その下は、$limit の値になります。
my $limit = int(($num - eval(join '+', 0 .. ($div - 1))) / $div);
$m,$n $limitの値
13,4 4
21,5 5
31,6 5
43,7 6
57,8 6
73,9 7
91,10 7
1 と 2 が分割済みで、次に分割する整数がすでに分割した整数の和プラス1 (4 = (1 + 2) + 1) よりも大きくなる (5 以上) と、円上にどのように配置しても加算式で 4 ができないことになってしまいます。 これを一般化すると、$limit の式は次のようにできます。
my $limit;
{ my $i = eval(join '+', @comb) + 1;
my $j = int(($num - eval(join '+', 0 .. ($div - 1))) / $div);
$limit = $i < $j ? $i : $j;
}
上のコードでは、3つ目に分割される整数は 3 か 4 になります。 4つ目に分割される整数は、すでに分割された整数が (1, 2, 3) のときは 4 から 7 まで、(1, 2, 4) のときは 5 から 8 までとなります。
comb で1組の分割が終了したら、順列を生成する perm を呼び出します。 分割されたリストには必ず1が含まれているので、a に割り当てることにしましょう。 perm では、a を除く数字の順列を生成することになります。単純に順列を生成して、 生成した順列をチェックすることで正解を得ることができます。 最初に作ったプログラムは、次のようなものです。
use strict;
my $n = 8;
my $max = $n * ($n -1) + 1;
comb($max - 3, 3, $n - 2, 2);
sub comb {
my ($num, $min, $div, @comb) = @_;
my $limit;
{ my $i = eval(join '+', 1, @comb) + 1;
my $j = int(($num - eval(join '+', 0 .. ($div - 1))) / $div);
$limit = $i < $j ? $i : $j;
}
foreach my $i ($min .. $limit) {
my @list = @comb;
push @list, $i;
if ($div == 2) {
push @list, $num - $i;
perm([1], \@list);
} else {
comb( $num - $i, $i + 1, $div - 1, @list);
}
}
}
sub perm {
my @order = @{shift()};
my @rest = @{shift()};
if (@rest == 1) {
push @order, $rest[0];
print join('_', @order), "\n" if check(@order);
} else {
foreach my $i (0 .. $#rest) {
push @order, $rest[$i];
my @tmp = @rest[0 .. $i - 1, $i + 1 ..$#rest];
perm(\@order, \@tmp);
pop @order;
}
}
}
sub check {
my @work = @_;
my %flag;
@flag{@work} = split //, '1' x @work;
my $i = @work;
while ($i--) {
foreach (1 .. ($#work - 1)) {
$flag{eval(join '+', @work[0 .. $_])}++;
}
@work = @work[1 .. $#work, 0];
}
if (join('', values %flag) =~ /^1+$/) { return 1; }
else { return 0; }
}このプログラムでは、すべての順列を生成して加算式の値の重複をチェックしているだけです。 サブルーチン check は、円上のすべての数字の加算式の値を除く、 残りのすべての加算式の値に重複がないときは1を返し、重複があるときは 0 を返します (円上のすべての数字の加算式の値は、他の加算式の値と重複しないので除外しても大丈夫です)。
実行時間は、円上に7個 ($n = 7) 配置したときは 52 秒、8個 ($n = 8) のときは 2068 秒と多くの時間がかかります。実行時間が多くかかる理由は、生成する順列数の多さにあります。$n が 7 (以降 $n: 7 と表記) では生成数が 55,440 (77 x 6!) となり、$n: 8 では 1,532,160 (707 x 7!) となってしまいます。 他にも、重複解の問題があります。$n: 8 のときの出力は、次のようになります ($n: 7 は、正解がない)。
$n: 8 1_4_22_7_3_6_2_12 1_12_2_6_3_7_22_4 1_6_12_4_21_3_2_8 1_8_2_3_21_4_12_6 1_4_2_10_18_3_11_8 1_8_11_3_18_10_2_4 1_3_5_11_2_12_17_6 1_6_17_12_2_11_5_3 1_3_8_2_16_7_15_5 1_5_15_7_16_2_8_3 1_2_10_19_4_7_9_5 1_5_9_7_4_19_10_2
最初の 1_4_22_7_3_6_2_12 と2番目の 1_12_2_6_3_7_22_4 (3,4番目、5,6番目、... も同様) は、一見すると重複解と見えないかもしれません。先頭の1を削除して、見比べてみてください。 逆順に並んでいるだけです。これは、円上に1を起点として右回りか左回りかの違いです。 この重複解は、2番目の数字と最後の数字を比較して (4 と 12、12 と 4) 最後の数字が小さいときにスキップすれば除外できます。しかしながら、順列を生成した後で除外しているので、 実行時間の短縮は望めません。もう少し、よい方法があります。1の右側に数字を1つつないだ後に、 左に右よりも大きな1つ数字をつなぎます。そして、それを引数にして perm を呼び出すように変更します。
sub comb {
my ($num, $min, $div, @comb) = @_;
my $limit;
{ my $i = eval(join '+', 1, @comb) + 1;
my $j = int(($num - eval(join '+', 0 .. ($div - 1))) / $div);
$limit = $i < $j ? $i : $j;
}
foreach my $i ($min .. $limit) {
my @list = @comb;
push @list, $i;
if ($div == 2) {
push @list, $num - $i;
foreach my $j (0 .. ($#list - 1)) {
foreach my $k (($j + 1) .. $#list) {
my @work = grep { ! /^$list[$j]$/ and ! /^$list[$k]$/ } @list;
perm([$list[$k], 1, $list[$j]], \@work);
}
}
} else {
comb( $num - $i, $i + 1, $div - 1, @list);
}
}
}
この変更で順列の生成数が半分になり、実行時間も約半分になります。 $n: 7 のときに実行時間は 27 秒 (52 -> 27) に減り、順列の生成数は 27,720 (55,440 -> 27,720) に減ります。$n: 8 では、実行時間が 1,041 秒 (2,068 -> 1,041)、順列生成数は 766,080 (1,532,160 -> 766,080) に減ります。 重複解が除外できて実行時間が短縮できるので、まさしく一石二鳥です。
さらに、順列の生成数の削減を続けます。3 以上の値は、円上に1つの数字としてある場合と加算によって得られる場合がありますが、3 と 4 を1つの組として見た場合に、次のような特徴があります。この特徴を利用して、コードに一工夫加えます。
3 と 4 が共にある (2, 3, 4, ...)
2 と 3 を1の隣りに配置すると値が重複してしまうので、1の隣り以外に配置する必要があります。
3 があって 4 がない (2, 3, 5以上, ...)
4 は、1と 3 の和で作り出されることになり、隣接して配置する必要があります。
3 がなくて 4 がある (2, 4, 5以上, ...)
3 がないので、1と 2 は隣接して配置する必要があります。
foreach my $j (0 .. ($#list - 1)) {
if ($list[1] == 3 and $list[2] == 4) {
next if $j == 0 or $j == 1;
} elsif ($list[1] == 3) {
next if $j == 0;
last if $j == 2;
} else {
last if $j == 1;
}
foreach my $k (($j + 1) .. $#list) {
my @work = grep { ! /^$list[$j]$/ and ! /^$list[$k]$/ } @list;
perm([$list[$k], 1, $list[$j]], \@work);
}
}
上の変更で、$n: 7 では実行時間が 9 秒 (52 -> 27 -> 9) に減り、順列生成数が 9,240 (55,440 -> 27,720 -> 9,240) に減りました。$n: 8 の場合は、実行時間が 359 秒 (2,068 -> 1,041 -> 359)、順列生成数は 264,480 (1,532,160 -> 766,080 -> 264,480) になりました。
2つの変更で、実行時間は大幅に短縮することができました。 さらなる実行時間の短縮を目指して、順列の生成の途中で枝刈りを検討してみましょう。 ここで考えられる枝刈りは、順列の生成の途中で加算値の重複をチェックすることです。 例として、円上に6個の数字を配置して、その分割リストが (1, 2, 3, 6, 9, 10) の場合を使って説明します。このリストの組み合わせは、最終的に失敗となります。
加算値の中には、重複しない加算値というものがあります。1 と 2、すべての数字の合計値 ($max)、$max から 1 と 2 を引いたもの (1, 2, $max - 1, $max -2, $max) がそれに当たります。 これについては、加算値の重複チェックから外すことができます。 また、加算値の中には、配置せずに分割リストを生成した段階で分かるものがあります。 各数字とすべての数字の合計値はむろんですが、すべての数字の合計値から各数字を引いたものもそれに当たります。 まず分割リストを生成したら、加算値の重複をチェックするための配列 @overlap を作ります。
@overlap = map { $_, $max - $_ } @list[1 .. $#list];
1, (2, 3, 6, 9, 10): 3, 28, 6, 25, 9, 22, 10, 21 # 1, 2, 29, 30, 31 は省略
数字6つを円上に並べる順列の生成では、a を1に固定して、次に b、その次に f、その後は c, d, e と並べて行きます。
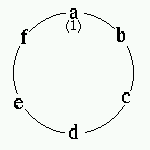
最初に並べる b と a の加算値は、3 と 4 のいずれか一方がある分割リストでは、重複はなくチェックの必要がありません。 3 があって 4 がないときは 4 を作るために b に 3 を並べ、3 がなくて 4 があるときは 3 を作るために b に 2 を並べるからです。3 と 4 がともにある分割リストでは 4 以降の数字を b に並べますが、(1, 2, 3, 4, 5, ...) のような場合に 4 を b に並べると a+b が 5 となり加算値が重複します。
# 3 と 4 の両方がある場合のみ加算値の重複をチェックする
if ($list[1] == 3 and $list[2] == 4) {
next if $j == 0 or $j == 1;
my $chk = 1 + $list[$j]
next if grep /^$chk$/, @overlap;
} elsif ($list[1] == 3) {
next if $j == 0;
last if $j == 2;
} else {
last if $j == 1;
}
例として取り上げた (1, 2, 3, 6, 9, 10) では、分割リストに 4 がないので a に1が、b に 3 が並べられて 1_3 となります。次に残りのリストから 3 よりも大きい 6 が1の左に並べられ、6_1_3 のようになります。ここで、チェック用のサブルーチン check を呼び出します。
sub check {
my @list = @_;
my @work;
foreach (1 .. $#list) {
last if $#list == $n - 2 and $_ == $#list; # 「$max - 各数字」をスキップ
my $add = eval(join '+', @list[0 .. $_]);
return 0 if grep /^$add$/, @overlap; # 加算値が重複した
push @work, $add;
}
return \@work; # 加算値の重複はない
}
check では、新しく並べた 6 と 1_3 との加算値 7(6+1), 10(6+1+3) が @overlap にないか調べます。10 が @overlap の中にあるので失敗ということになり、次に 9 を1の左に並べて check を呼び出しますが、これも失敗します。その次の 10 は加算値に重複がなく、成功ということになります。 成功の場合は、@overlap に加算値を追加します。 このようなことが、結果が出るまで続けられます。以下は、その様子です。
加算値 @overlap
6_1_3 (2, 9, 10): 7, 10 3, 28, 6, 25, 9, 22, 10, 21, 4 # 失敗
9_1_3 (2, 6, 10): 10, 13 3, 28, 6, 25, 9, 22, 10, 21, 4 # 失敗
10_1_3 (2, 6, 9): 11, 14 3, 28, 6, 25, 9, 22, 10, 21, 4 # OK、@overlap の末尾に 11, 14 を追加
10_1_3_2 (6, 9): 5, 6, 16 3, 28, 6, 25, 9, 22, 10, 21, 4, 11, 14 # 失敗
10_1_3_6 (2, 9): 9, 10, 20 3, 28, 6, 25, 9, 22, 10, 21, 4, 11, 14 # 失敗
10_1_3_9 (2, 6): 12, 13, 23 3, 28, 6, 25, 9, 22, 10, 21, 4, 11, 14 # OK
10_1_3_9_2 (6): 11, 14, 15 3, 28, 6, 25, 9, 22, 10, 21, 4, 11, 14, 12, 13, 23 # 失敗
10_1_3_9_6 (2): 15, 18, 19 3, 28, 6, 25, 9, 22, 10, 21, 4, 11, 14, 12, 13, 23 # OK
10_1_3_9_6_2 (): # 同じチェックではダメ
最後の 2 を並べたときに check の呼び出しでは、加算値のチェック洩れが生じます。 check では数字2個の加算値は 8(2+6) だけがチェックされますが、円が繋がったため 12(10+2) もチェックする必要があります。数字3、4個の加算値も同様です。
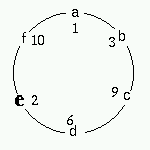 | @overlap(省略加算値も含む) 未チェックの加算値 a, b, c, d, e, f f+a, a+b, b+c, c+d d+e, e+f f+a+b, a+b+c, b+c+d c+d+e, d+e+f, e+f+a f+a+b+c, a+b+c+d b+c+d+e, c+d+e+f, d+e+f+a, e+f+a+b a+b+c+d+e, b+c+d+e+f, c+d+e+f+a d+e+f+a+b, e+f+a+b+c, f+a+b+c+d a+b+c+d+e+f |
太字で示してある e が最後に配置され、円が繋がったことによって e が含まれるすべての加算値を取得する必要があります。check では太字で示してある加算値だけがチェックされ、残りのものは抜けてしまいます。 そのため最後のチェックだけは、perm の中で行うようにしてあります。
sub perm {
・・・
if (@rest == 1) {
my @list = ($rest[0], @order);
my @work,
my $i = $#list - 1;
my $j = 0;
while ($i--) {
foreach (($j ? $j : 1) .. ($#list - 2)) {
my $add = eval(join('+', @list[0 .. $_]));
return if grep /^$add$/, @overlap, @work;
push @work, $add;
}
@list = @list[$#list, 0 .. $#list - 1];
$j++;
}
push @order, $rest[0];
print join('_', @order[1 .. $#order], $order[0]), "\n";
} else {
・・・
}
}
この部分のコードは、初めは未チェックの加算値だけを得るアルゴリズムが分からず、 かなり苦心しました。配列をずらしながら $j 変数を制御することで、何とか実現できました。外側の while は、配列を $i が 0 になるまでずらします。内側の foreach で加算値を得て、重複をチェックしています。
$i @list $j foreach 得られる加算値 4 e, f, a, b, c, d 0 1 .. 3 e+f, e+f+a, e+f+a+b 3 d, e, f, a, b, c 1 1 .. 3 d+e, d+e+f, d+e+f+a 2 c, d, e, f, a, b 2 2 .. 3 c+d+e, c+d+e+f 1 b, c, d, e, f, a 3 3 b+c+d+e
以上の説明の枝刈りで、$n: 7 では実行時間が 1 秒 (52 -> 27 -> 9 -> 1) に減り、順列生成数が 168 (55,440 -> 27,720 -> 9,240 -> 168) に減りました。$n: 8 の場合は、実行時間が 7 秒 (2,068 -> 1,041 -> 359 -> 7)、順列生成数は 1,325 (1,532,160 -> 766,080 -> 264,480 -> 1,325) になりました。
$n: 4 $n: 5 $n: 6 $n: 7 $n: 8, 7秒
1_3_2_7 1_3_10_2_5 1_7_3_2_4_14 解なし 1_4_22_7_3_6_2_12
1_2_6_4 1_3_6_2_5_14 1_6_12_4_21_3_2_8
1_3_2_7_8_10 1_4_2_10_18_3_11_8
1_2_5_4_6_13 1_3_5_11_2_12_17_6
1_2_7_4_12_5 1_3_8_2_16_7_15_5
1_2_10_19_4_7_9_5
$n: 9, 118秒 $n: 10, 2,222秒 $n: 11, 40,133秒
1_4_7_6_3_28_2_8_14 1_5_4_13_3_8_7_12_2_36 解なし
1_11_8_6_4_3_2_22_16 1_6_9_11_29_4_8_2_3_18
1_6_4_24_13_3_2_12_8 1_4_3_10_2_9_14_16_6_26
1_2_4_8_16_5_18_9_10 1_4_2_20_8_9_23_10_3_11
1_3_9_11_6_8_2_5_28_18
1_2_6_18_22_7_5_16_4_10
(2006/08/01)