数字並べ

さて、今回の問題は数字並べです。数字は、１から N までの２組使います。言葉で説明するよりも、例を見てもらいましょう。下の例は、１から４まで並べたものです。

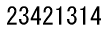
１と１の間には他の数字が１つ、２と２の間には他の数字が２つ、３と３の間には他の数が３つ、４と４の間には他の数字が４つ、というように並んでいます。では１から７までの数字２組を使って、同じルールで並べ下さいというのが、今回の問題です。

プログラム

use strict;
my ($count, @result);
my $max = 7;
my $lens = $max * 2;

search($max, 0);

sub search {
  my ($num, $added) = @_;
  my $work = $num . '0' x $num . $num;
  my $flag = $work; $flag =~ s/0/./g;
  foreach (0..($lens - length($work))) {
    my $tmp = $work . '0' x $_;
    my $add = $added + $tmp;
    if ($add =~ /$flag/) {
      if ($num == 1) {
        my $turn = reverse $add;
        last if grep /$turn/, @result;
        push @result, $add;
        $count++;
        last;
      } else {
        search($num - 1, $add);
      }
    } else {
      next;
    }
  }
}

if ($count) {
  print join("\n", @result), "\n";
  print "解の数: $count\n";
} else {
  print "$max: 解なし\n";
}

プログラムの説明

さて今回の問題は、どのようにしたら解けるでしょうか？順列を生成してしらみ潰しに正解を見つける方法もありますが、桁数が 14 になりますのでそれも難しいでしょう。しばらく考えていましたが、ある時に、単純な足し算に還元できることを思いつきました。次の式は、最初に取り上げた 1 から４までの例を分解したものです。

上の左側は、正解から同じ数字を抜き出して、間と末尾の他の数字を 0 に置き換えたものです。当然それを足し算すると、正解が得られますね。ですから正解を得るためには、右側に示してあるように、末尾の 0 の数の組み合わせを調べればよいことがわかります。このアルゴリズムを実現したのが、上のプログラムです。

プログラムとしては、ごく易しいものなので簡単に説明します。プログラムの中心部は、search サブルーチンで、それがすべてです。その search サブルーチンの大まかな流れは、以下の通りです。

それでは、プログラムを実行してテストしてみます。 $max に 3 から 9 までの数値を指定したときの出力は、以下の通りです。

3 と 4 には、解が１つ (重複解を含めると２つ) あります。5 と 6 には解がなく、7 には 26 の解があります。また、8 と 9 には解がありません。これで、今回は終わりのはずでしたが ..... 。

実は、上の出力には誤りがあります。本当は、8 には解があります (9 の場合は、過程に誤りがあるが結果的には正しい)。プログラムの実行の様子を覗いて見ると、思いがけないところに意外な落とし穴がありました。原因は、足し算の過程で桁数が 16 桁になると、指数表記になってしまうためと分かりました (この点については、Perl の実行環境によって異なるのかも知れませんが)。原因が分かったところで、プログラムを修正してみましょう。ここでは、興味深い方法がありますので、それを紹介します。

use strict;
my ($count, @result);
my $max = 8;
my $lens = $max * 2;

search($max, '0' x $lens);

sub search {
  my ($num, $added) = @_;
  my $work = $num . '0' x $num . $num;
  my $flag = $work; $flag =~ s/0/./g;
  foreach (0..($lens - length($work))) {
    my $tmp = $work . '0' x $_;
    $tmp = '0' x ($lens - length($tmp)) . $tmp;
    my $add = "$added" | "$tmp";
    if ($add =~ /$flag/) {
      if ($num == 1) {
        my $turn = reverse $add;
        last if grep /$turn/, @result;
        push @result, $add;
        $count++;
        last;
      } else {
        search($num - 1, $add);
      }
    } else {
      next;
    }
  }
}

if ($count) {
  print join("\n", @result), "\n";
  print "解の数: $count\n";
} else {
  print "$max: 解なし\n";
}

元のプログラムからの変更箇所は、太字で表示してあります。ほんの少しの変更です。元のプログラムで足し算で行っていたところを、このプログラムでは文字列同士の論理和で行っています。私自身も今まで一度も使ったことがなく、おぼろげに覚えていただけでした。文字列同士の論理和を使う場合には、文字数 (桁数) を揃えることと、明示的に文字列として指定する必要があります。文字列同士の論理和は、同じ位置にある文字同士の文字コードの論理和がとられます。ちなみに、数字の文字コードは以下の通りになります。

上の文字コードを見ると、0 と他の数字の論理和をとると他の数字になることが分かります。ですから、0 + 1 と "0" | "1" は、同じ結果が得られます。なお、今回のプログラムのチェック ($add =~ /$flag/) のコードの場合には、大きな数字から論理和をとる必要があります。例えば 5 の場合、6 以上の数字と論理和をとると必ず 5 以外になりますが、4 以下の数字と論理和をとると 4 と 1 では結果が 5 となり、0 と論理和をとったか否かが不明になります。

今度こそ、本当に終わりです。最後に、$max が 8 のときの出力結果を示します。