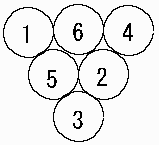
今回のパズルは、逆三角形に並べた円 (6, 10 15 個) に数字を配置する問題です。 下の図は、逆三角形に並べた円6つに1から6を配置したものです。 下の円は、上2つの円の数字の差になっています。

今回のパズルは、何を手掛かりにして解いたらいいか少し分かりませんでした。 結局は、最大の数字は1番上の段に配置されますので、その数字を含む順列を生成して1番上の段に配置して、 2番目の段からは計算で求めるプログラムにしました。ちなみに、難しい理屈は分かりませんが、 6段以上の逆三角形には解がないそうです。良かったというべきかも..... 。
use strict;
my $m = 10; # 6 or 10 or 15
my @elms = (11);
while (@elms < $m) {
if ($elms[0] =~ /(.)\1/) { unshift @elms, ((split //, $elms[0])[0] . '1') + 10; }
else { unshift @elms, $elms[0] + 1; }
}
my $top = (split //, $elms[0])[0] - 3;
my (@work, $head, $tail);
foreach my $i (1 .. $m - 2) {
foreach my $j ($i + 1 .. $m - 1) {
$head = $i; $tail = $j;
if ($top == 0) {
check($head, $tail, $m);
check($head, $m, $tail);
check($m, $head, $tail);
} else {
perm(grep { ! /^$head$/ and ! /^$tail$/ } 1 .. $m - 1);
}
}
}
sub perm {
my @nums = @_;
foreach my $i (0 .. $#nums) {
push @work, $nums[$i];
if (@work == $top) {
my @tmp = ($head, @work, $tail);
my $n = $m - 1;
if (grep /^$n$/, @tmp) {
foreach (0 .. $#tmp + 1) {
my @temp = @tmp;
splice @temp, $_, 0, $m;
check(@temp);
}
} elsif (grep /^1$/, @tmp) {
my $index; my $j = 0;
foreach (@tmp) {
if (/^1$/) {
$index = $j;
last;
}
$j++;
}
my @temp = @tmp;
splice @temp, $j, 0, $m;
check(@temp);
my @temp = @tmp;
splice @temp, $j + 1, 0, $m;
check(@temp);
}
} else {
perm(@nums[0 .. $i - 1, $i + 1 .. $#nums]);
}
pop @work;
}
}
sub check {
my @tmp = @_;
my %result;
@result{@elms} = @tmp;
my (@before, $i, $j, $k, $l); $i = $elms[0]; $j = $i - 1; $k = $j - 10;
@before = @tmp;
while ($j > 11) {
$l = abs($result{$i} - $result{$j});
if (grep /^$l$/, @before) { return; }
else {
$result{$k} = $l; push @before, $l;
if ($i =~ /2$/) {
$i = ((split //, $i)[0] - 1) . ((split //, $i)[0] - 1);
$j = $i - 1; $k = $j - 10;
} else {
$i--; $j--; $k--;
}
}
}
my $hs = ' ';
foreach (sort { $b <=> $a } keys %result) {
print "$result{$_} " if $_ =~ /[^1]$/;
if ($_ =~ /1$/) {
print "$result{$_}\n$hs";
$hs .= ' ';
}
}
print "\n";
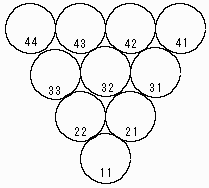
}ここからは、円の数を 10 個配置した逆三角形を例にして話を進めていきます。 まずは、円の1つ1つに番号を付けます。番号は、下の図のように付けます。10 の位は段の位置を表し、1の位は右から数えた位置を表します。
 |
my @elms = (11);
while (@elms < $n) {
if ($elms[0] =~ /(.)\1/) { unshift @elms, ((split //, $elms[0])[0] . '1') + 10; }
else { unshift @elms, $elms[0] + 1; }
} |
図の右側は、自動的に円に番号を生成するコードです。コードを実行すると @elms には、円の番号 44, 43, ... 21, 11 が格納されます。 このコードは、9段までの逆三角形の円に番号を付けることができます。 また @elms の先頭の要素を見れば、正しい逆三角形になっているか判別することもできます。@elms の最初の要素は、正しい逆三角形では同じ数字のゾロ目になります。
次は、順列を生成して最上段 44, 43, 42, 41 に数字を配置します。 順列生成のコードは、最初は単純な以下のようなものでした。
my $m = 10; my $n = (split //, $elms[0])[0];
my @work = ();
search(1 .. $m);
sub search {
my @list = @_;
foreach my $i (0 .. $#list) {
push @work, $list[$i];
if (@work == $n) {
check(@work) if $work[0] < $work[-1];
} else {
search(@list[0 .. $i - 1, $i + 1 .. $#list]);
}
pop @work;
}
}
上のコードでは、円が6個の場合には 120、円が 10 個の場合には 5040、円が 15 の場合には 360360 個の順列が生成されます。円の数が6個と 10 個の場合は、プログラムはすぐに終了します。 しかしながら、円が 15 の場合は、私のパソコンで 29 秒くらい掛かってしまいました。
そこで、もう少し工夫することにしました。ここで、順列の性質を考えてみましょう。 順列は、正並びの順列と逆並びの順列が1つの組になっています。1, 2, 3, 4 の正並びの順列に対する、4, 3, 2, 1 という逆並びの順列が必ず存在します。今回のパズルでは、重複解となるので片方を除外する必要があります。 上のコードの if $work[0] < $work[-1] は、逆並びの順列を除外するためのものです。しかしながら、上のコードでは生成した後で除外しています。 この逆並びの順列を最初から生成しなければ、半分の時間で実行できることになります。 次のコードは、正並びの順列のみを生成するものです。
foreach my $i (1 .. $m - 1) {
foreach my $j ($i + 1 .. $m) {
# $i と $j を除外した残りの数字の順列を生成する
}
}
$i は先頭の数字、$j は末尾の数字になります。$i と $j を除いた残りの数字の順列を生成して、$i と $j の間に入れます。これで、正並びの順列のみを生成できます。
次に、最大値の $m について考えてみましょう。$m は、必ず最上段に入ります。 そこで、1つ小さいサイズの順列を生成して、後から $m を配置するようにすれば、 生成する順列数を少なくすることができます。次に大きな値の ($m - 1) は、最上段に入るか、あるいは最上段が $m, 1 (または 1, $m) になっている必要があります。この点についても、チェックするようにしています。 今回のパズルの順列の生成の仕組みは、以上の通りです。 これで、円の数が 15 個の場合も、4秒くらいでプログラムが終わるようになりました。
順列を生成したら、check サブルーチンを呼び出します。check サブルーチンでは、渡された引数を %result ハッシュに格納します。%result のキーは円の番号で、値は配置される数字になります。 渡された引数は最上段の数字だけですので、最初の %result は下図のようになります。
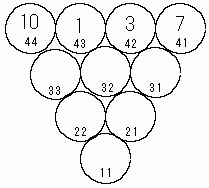 | 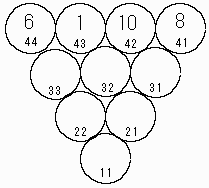 | |
| 失敗の例 | 成功の例 |
上から2段目からの円の数字は、計算によって求めていくことになります。 その部分のコードを、以下に再掲します。
my (@used, $i, $j, $k, $l); $i = $elms[0]; $j = $i - 1; $k = $j - 10;
@used = @tmp;
while ($j > 11) {
$l = abs($result{$i} - $result{$j});
if (grep /^$l$/, @used) { return; }
else { $result{$k} = $l; push @used, $l; }
if ($j =~ /1$/) {
$i = ((split //, $i)[0] - 1) . ((split //, $i)[0] - 1);
$j = $i - 1; $k = $j - 10;
} else {
$i--; $j--; $k--;
}
}
まず最初に、必要な変数を定義します。@used には、すでに使用済みの数字を格納しておきます。この @used を使って、計算によって得られた値の数字が重複していないかを確認します。上から2段目からの数字は、while を使って配置していきます。上の図の "失敗の例" では、円の番号 33 から 9, 2, 4 と数字を配置していき、22 に 7 を配置しようとしたときに、数字が重複しているために失敗します。右側の図では、11 まで数字を配置できますので、正解ということになります。
プログラムの実行結果は、以下のようになります。
$m = 6 $m = 10 $m = 15
1 6 4 6 10 1 8 6 14 15 3 13
5 2 4 9 7 8 1 12 10
3 5 2 7 11 2
3 4 9
6 1 4 5
5 3 6 1 10 8
2 5 9 2
4 7
2 6 5 3
4 1
3 8 10 3 9
2 7 6
6 2 5 5 1
4 3 4
1
8 3 10 9
5 7 1
2 6
4
(2005/11/01)