数入れパズル

今回は、円上に配置してある小さな円の中に数字を入れるパズルです。下図は、円上に６つの小さな円があります。まず最初は、Start に示してある位置から数字を入れていきます。入れることのできる数字は、１から小さな円の個数未満 (図の場合は、1, 2, 3, 4, 5) のうちの１つです。数字を入れたら、その数字の数だけ矢印の方向に移動します。次の位置からは、すでに配置済みの数字を除いた残った数字から選びます。最後の位置に到着したら、もう移動することはできませんので 0 を入れます。なお、同じ位置には１度しか立ち寄れません。このようにして、すべての数字を配置することができれば成功です。

プログラム

use strict;
my $n = 6;
my (@state, @result);
$state[$_] = '0' foreach (0 .. ($n - 1));
my $goal = eval(join '+', 1 .. ($n - 1)) % $n;
my @move =  1 .. ($n - 1);
search('0', @move);

sub search {
  my $cp = shift;
  my @move = @_;
  foreach my $i (@move) {
    my $np = ($cp + $i) % $n;
    next if $state[$np] != 0;
    next if @move >= 2 && $np == $goal;
    $state[$cp] = $i;
    if (@move == 1 && ! $state[$np]) {
      push @result, [@state];
    } else {
      search($np, grep !/^$i$/, @move);
    }
    $state[$cp] = '0';
  }
}

my ($line_1, $line_2) = ('', '');
foreach (0 .. $#result) {
  my @work = @{$result[$_]};
  my $work_line_2 = join ' ', reverse @work[1 .. $#work];
  my $left_margin  = ' ' x int((length($work_line_2) - 1) / 2);
  my $right_margin = ' ' x (length($work_line_2) - length($left_margin) - length($work[0]));
  if ($line_1 eq '') {
    $line_1 = $left_margin . $work[0] . $right_margin;
    $line_2 = $work_line_2;
  } else {
    $line_1 = $line_1 . "     " . $left_margin . $work[0] . $right_margin;
    $line_2 .= "     $work_line_2";
  }
  if ($i == $#result) {
    print "$line_1\n\n$line_2\n\n\n";
    last;
  }
  if (length($line_2) + length($work_line_2) > 75) {
    print "$line_1\n\n$line_2\n\n\n";
    $line_1 = $line_2 = '';
  }
}

プログラムの説明

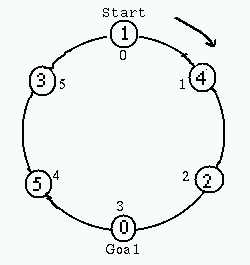
今回のパズルでは、円に配置してある小円の数が奇数の場合は正解がありません。パズルの性質上、ゴールの位置は最初から決まっています。下の図は、小円の数が６個の場合の正解の１つです。ゴール以外の小円には１から 5 までの数字が入り、その合計値がゴールの位置になります。

小円の数が６つの場合は、合計値が 15 になるので、ゴールは 3 の位置になります。これを一般化すると、円上に小円が偶数個配置されている場合は、配置されている小円の数の半分の位置 ($n / 2) になります。すなわち、start の小円に向かい合っている小円がゴールの位置になります。

円上に小円が奇数個配置されている場合には、ゴールの位置が 0 になってしまいます。このことは、すべての小円に数字を入れることができないことを意味しています。このプログラムで $n に奇数を指定した場合は、実行はされるものの何も出力しません。

小円に数字を入れる作業は、search サブルーチンを再帰呼び出ししながら行います。小円のデータの管理は、配列 @state が受け持ちます。配列の添字が小円の位置番号を表し、要素が移動した数字を表します。@state は、最初にすべて '0' で初期化しておきます。search サブルーチンの引数は、現在の小円の位置と次に移動できる数字のリストです。search サブルーチンの基本構造は、次のようになります。

正解は配列 @result に保存しておいて、プログラムの最後に整形して出力します。出力部分のコードは易しいので、説明は省略します。正解の表示は、簡略化してスタートのみ別に表示して、残りは１行で表示しています。プログラムの実行結果は、次のようになります。

円上に配置する小円の数がいくつでも、正解が１つのものはありません。しかも、小円の数が増えるに従い正解の数が増えてしまいます。小円の数が 12 の場合は、実に正解の数が 3856 になります。実際のパズルとしては、数個の数字入れておいて、残りを入れてもらうのがよいのかもしれません。例えば、小円の数が６個の場合に、スタート位置にあらかじめ入れておくと、正解が１つだけしかないパズルに変身させることができます。

逆並びの順列を除外した順列の生成

まず先にお断りしておきますが、逆並びの順列という定義があるわけではありません。完全順列の順列の１つには、反転した場合に同じなる順列 (これを逆並びの順列と呼ぶ) が必ず存在します。例えば、数字 1, 2, 3, 4 の完全順列には、1 2 3 4 に対応する 4 3 2 1 という並びが存在します。どのような並びの順列にも、このような逆な並びの順列が存在します。この逆並びの順列は、パズルでは重複解となって現れることがあります。最初からこの逆並びの順列を除外した順列を生成できれば、便利なこともあります。次は、簡単な順列生成プログラムです。

script_1
  use strict;
  my $m = 4; my $n = 4;
  my @work = ();
  search(1 .. $m);

  sub search {
    my @list = @_;
    foreach my $i (0 .. $#list) {
      push @work, $list[$i];
      if (@work == $n) {
        print @work, "\n";
      } else {
        search(@list[0 .. $i - 1, $i + 1 .. $#list]);
      }
      pop @work;
    }
  }

上のプログラムは、１から $m までの数字から $n 個の順列を生成するものです。 $m = 10; $n = 4; とすると、１から 10 までの数字の中から４個の数字の順列が生成されます。上のプログラムでは、$m = 4; $n = 4; としています。実行すると、ソート順 (ASCII 順) に以下の順列が生成されます。

上の順列の内、先頭にアスタリスク "*" が付いたものが逆並びの順列です。この逆並びの順列を除外した順列を生成するには、どのようにすればよいでしょうか。逆並びの順列を観察すると、先頭の数字が末尾の数字よりも大きいことに気付きます。そこで、手っ取り早い方法は次のようになります。

script_2
  use strict;
  my $m = 4; my $n = 4;
  my @work = ();
  search(1 .. $m);

  sub search {
    my @list = @_;
    foreach my $i (0 .. $#list) {
      push @work, $list[$i];
      if (@work == $n) {
        print @work, "\n" if $work[0] < $work[-1];
      } else {
        search(@list[0 .. $i - 1, $i + 1 .. $#list]);
      }
      pop @work;
    }
  }

このプログラムを実行すると、上の出力例の逆並びの順列が除外されて、正並びの順列のみ生成されます。このプログラムの問題点は、すべての順列を生成した後で逆並びの順列を除外していることです。そのため、実行時間は短くなりません。実行時間を短く (半分に) するためには、最初から逆並びの順列を生成しないようにする工夫が必要です。

先に述べたように逆並びの順列は、先頭の数字が末尾の数字よりも大きくなっています。この点に着目して、上のプログラムを改造して作ってみました。

script_3
  use strict;
  my $m = 4; my $n = 4;
  my (@work, $head, $tail);

  foreach my $i (1 .. $m - 1) {
    foreach my $j (reverse($i + 1 .. $m)) {
      $head = $i; $tail = $j;
      perm(grep { ! /^$i$/ and ! /^$j$/ } 1 .. $m);      
    }
  }

  sub perm {
    my @nums = @_;
    foreach my $i (0 .. $#nums) {
      push @work, $nums[$i];
      if (@work == ($n - 2)) {
        print "$head @work $tail\n";
      } else {
        perm(@nums[0 .. $i - 1, $i + 1 .. $#nums]);
      }
      pop @work;
    }
  }

このプログラムの欠点は、生成される順列がソート順にならないことです。いろいろと考えてみましたが、うまい方法は見つかりませんでした。