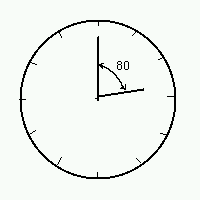
今回は、短くてやさしいプログラムを2つ取り上げます。 最初のプログラムは、「指定した時計の針の角度の時刻」を表示するものです。 針の角度は、長針から時計回りに測定した角度です。以下は、「次回の予定」で掲載した図です。

問題は、「長針が 12 の目盛りの内の1つを指していて、短針との角度が 80 度の場合、何時何分でしょうか」というものでした。パズルとしてはきわめてやさしいもので、 短針と短針の直前の目盛りとの角度を割り出すことで求めることができます。正解は、10 時 40 分となります。今回のプログラムで、角度を 80 度に指定して実行すると次のように表示されます。
Angle 80 00:50:54 6/12 01:56:21 9/12 03:01:49 1/12 04:07:16 4/12 05:12:43 7/12 06:18:10 10/12 07:23:38 2/12 08:29:05 5/12 09:34:32 8/12 *10:40:00 0/12 11:45:27 3/12
角度 80 度になる時刻は、すべて表示されます。先頭に '*' の付いた時間は、長針が 12 の目盛りの内の1つを指していることを表します (末尾の '?/12' については後述)。
use strict;
my $angle = 0;
print "Angle $angle\n";
my $angle = $angle * 120;
my $long = $angle ? 43200 - $angle : 0;
my $short = $angle ? (43200 - $angle) / 12 : 0;
while ($short < 43200) {
my $diff = ($long > $short) ? (43200 - $long) + $short : $short - $long;
if ($diff - $angle < 11) {
my $mark = $short % 300 ? ' ' : '*';
my ($hour, $minute, $second) = (int($short / 3600), int(($short % 3600) / 60), $short % 60);
printf "%s%02d:%02d:%02d %2d/12\n", $mark, $hour, $minute, $second, $diff - $angle;
$short += 3600;
}
$short += 1;
$long += 12;
$long = 0 if $long == 43200;
}プログラムは、ちょっとしたアイデアに基づいて作っています。通常の時計の文字盤は 12 の目立つ目盛りとその間の秒に相当する目立たない目盛りからなっていますが、 プログラムでは下図のような目盛りの文字盤を想定しています。
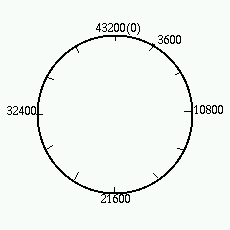
目盛りのすべてを図示することはできませんが、その数は 43,200 です。この 43,200 という数字は、短針が文字盤を1周する秒数 (60 x 60 x 12) です。 この文字盤を使うと、角度の探索を簡単に行うことができます。まず長針 ($long) と短針 ($short) に 0 をセットして、短針を1目盛り (1秒) ずつ、長針を 12 目盛りずつ進めながら角度をチェックしていきます。そして、短針が1回転すれば、探索は終了します。
while ($short < 43200) {
# ここで角度をチェックする
$short += 1;
$long += 12;
$long = 0 if $long == 43200;
}
探索する角度のチェックは、角度を目盛りの数に変換して行います。 目盛りの数への変換は、「角度 x 120」とします (43,200 ÷ 360 = 120)。 角度をチェックするコードは、次のようなものです。
while ($short < 43200) {
my $diff = ($long > $short) ? (43200 - $long) + $short : $short - $long;
if ($diff - $angle < 11) {
my $mark = $short % 300 ? ' ' : '*';
my ($hour, $minute, $second) = (int($short / 3600), int(($short % 3600) / 60), $short % 60);
printf "%s%02d:%02d:%02d %2d/12\n", $mark, $hour, $minute, $second, $diff - $angle;
$long += 3600; # この行と次の行はループを効率化させるためのコード
$short += (3600 + 3600 / 12);
}
...
}
$diff は現在の角度を、$angle は探索する角度です。ここで if ($diff == $angle) としてしまうと、秒間 (秒未満に端数がある) で探索する角度になる場合を検出できません。そこで、if ($diff - $angle < 11) としています。そして '?/12' の形で、行の末尾に表示するようにしています。 しかし、この秒未満の '?/12' は正確なものではなく (長針を ?/12 進めると、短針も長針の 1/12 進むため)、「?/12強」という意味です。
長針と短針が重なる (角度 0) 時刻と、長針と短針が一直線 (角度 180) となる時刻は、次のようになります。
Angle 0 Angle 180 *00:00:00 0/12 00:32:43 7/12 01:05:27 3/12 01:38:10 10/12 02:10:54 6/12 02:43:38 2/12 03:16:21 9/12 03:49:05 5/12 04:21:49 1/12 04:54:32 8/12 05:27:16 4/12 *06:00:00 0/12 06:32:43 7/12 07:05:27 3/12 07:38:10 10/12 08:10:54 6/12 08:43:38 2/12 09:16:21 9/12 09:49:05 5/12 10:21:49 1/12 10:54:32 8/12 11:27:16 4/12
2番目の問題は、デュードニー作と言われる下図の覆面算です。 異なるアルファベットには、異なる数字が入ります。
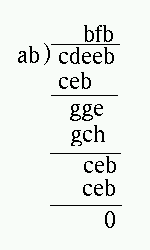
上の図を検討すると、次のことがわかります。a, b, f の順で数字を割り当てるとすると、
use strict;
foreach my $a (1 .. 9) {
foreach my $b (grep /[^$a]/, reverse 1 .. 9) {
last if eval("$a$b * $b") < 100;
foreach my $f (grep /[^$a$b]/, reverse 1 .. 9) {
last if eval("$a$b * $f") < 100;
my $cdeeb = eval("$a$b * $b$f$b");
next if $cdeeb !~ /([^$a$b$f])([^$a$b$f])([^$a$b$f])([^$a$b$f])$b/;
next if $1 == $2 or $1 == $3 or $2 == $3 or $3 != $4;
my $ceb = eval "$a$b * $b";
my ($c, $d, $e) = ($1, $2, $3);
next unless $ceb =~ /^$c$e$b$/;
my $gge = substr($cdeeb - $ceb * 100, 0, 3);
next unless $gge =~ /^([^$a$b$c$d$e$f])\1/;
my $g = $1;
my $gch = eval "$a$b * $f";
next unless $gch =~ /^$g$c([^$a$b$c$d$e$f$g])$/;
next unless ($gge . $b) - $gch * 10 == $ceb;
print " $b$f$b\n",
" ------\n",
"$a$b)$cdeeb\n",
" $ceb\n",
" ------\n",
" $gge\n",
" $gch\n",
" ------\n",
" $ceb\n",
" $ceb\n",
" ------\n",
" 0\n";
}
}
}プログラムはごく易しいものですので、見ていただければ理解できると思います。 ここでは、b と f に数字を割り当てる foreach のリストが逆順になっている理由のみを説明します。
foreach my $a (1 .. 9) {
foreach my $b (grep /[^$a]/, 1 .. 9) {
$count++;
next if eval("$a$b * $b") < 100;
...
}
}
上は、b に割り当てる数字を正順に並べたものです。ab x b は3桁になる必要がありますが、リストを正順に並べると next でスキップするほかありません。すべてのループを実行するので、$count の値は 72 になります。
foreach my $a (1 .. 9) {
foreach my $b (grep /[^$a]/, reverse 1 .. 9) {
$count++;
last if eval("$a$b * $b") < 100;
...
}
}
今度はリストを逆順に並べてあるので、ab x b が3桁にならなかった数字でループを last で打ち切ることができます。この場合、$count は 64 になります。ループの効率が少しですが、向上しています。 また、f も b と同じように foreach のリストを逆順にしています。b と f を正順にした場合のループ回数は 504 ですが、逆順にした場合は 359 になります。
プログラムの実行結果は、以下のようになります。
565
------
35)19775
175
------
227
210
------
175
175
------
0
正規表現では、思わぬ落とし穴があります。ここで取り上げる「前方参照直後の変数」も、 そのうちの1つになります。上の覆面算のプログラムに、次のような正規表現があります。
next if $cdeeb !~ /([^$a$b$f])([^$a$b$f])([^$a$b$f])([^$a$b$f])$b/; next if $1 == $2 or $1 == $3 or $2 == $3 or $3 != $4;
変数 $cdeef はその名前が表すとおり、3文字目と4文字目は同じ文字 (数字) でなければなりません。正規表現では、前方参照で前に出現した文字列を参照できます。 そこで正規表現を、次のように変えたらどうなるでしょうか?
next if $cdeeb !~ /([^$a$b$f])([^$a$b$f])([^$a$b$f])\3$b/; next if $1 == $2 or $1 == $3 or $2 == $3;
この正規表現は、結果的に失敗します。その理由を知るには、正規表現で \num がどのように解釈されるかを理解している必要があります。 正規表現文字列は、ダブルクォート「風」文字列として前処理されます。 「風」の意味は、ダブルクォート文字列とほぼ同じに処理されますが、 細かなところで少し違っている箇所があるということです。その違いの1つに、\num の扱いがあります。ダブルクォート内で \num は8進指定文字として解釈されますが、 正規表現内では8進指定文字と解釈される他に、前方参照としても解釈されます。 どちらに解釈されるかは、正規表現の文脈によります。
\1 .. \9
数字1桁の場合は、前方参照として解釈されます。
対応する丸括弧が前になければ、次のようなエラーメッセージが表示され、プログラムは中止されます。
reference to nonexistent group at ...
なお \0num のように書くと、数字の如何にかかわらず8進指定文字として解釈されます。
\10 以上
2桁以上の数字では、対応する丸括弧があれば前方参照として、ない場合は8進指定文字として解釈されます。\12
のように書くと、前方参照のつもりであっても、丸括弧が不足すればエラーにならず8進指定文字となります。
ここで、簡単な例を示しましょう。
$str = "abbcd"; $char = "c";
$str =~ /(.)\1$char/; # マッチする
上の例は、正常に正規表現が働きます。/(.)\1$char/ を前処理して変数を展開すると、/(.)\1c/ となります。このように変数を展開して数字でなければ、この正規表現は正常に働きます。では、次の例ではどうでしょうか。
$str = "abb5d"; $char = "5";
$str =~ /(.)\1$char/; # マッチしない
今度は、変数が展開されて /(.)\15/ になります。 この正規表現は、「任意の同じ文字が2つ続いた後に 5 の文字列」ではなく、「任意の1文字の後に8進指定文字 \15 の文字列」にマッチするようになってしまいます。この場合、正規表現が意図どおりに働かなくても、 構文としては正しいので warnnings を有効にしても検出できません。
以上説明したように、前方参照の直後に変数が続く場合は細心の注意が必要です。 特に大量にデータを処理して希にしか変数の内容 (先頭部分) が数字にならないケースでは、 見落としてプログラムのバグになってしまいます。
(2007/02/15)