連環の数

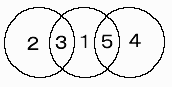
今回は、連なった円に数字を入れるパズルです。円の重なった部分の数字には、両隣の数字の和が入ります。円が３つの場合は、１から 5 の数字が入ります。解の１つは、下図のようになります。

円を１つ増やすと、入れる数は２つ増えます。円が４つの場合は、１から 7 の数字が入ります。今回のプログラムでは、円が 9 くらい (1 から 17) まではストレスなく解が得られます。それ以上の数でも、解は得られますが少し時間が掛かるようになります。

プログラム

use strict;
my $max = 9;
my ($count, @peices);

for (my $i = 1; $i < $max; $i++) {
  for (my $j = 1; $j < $max; $j++) {
    next if $i == $j;
    push @peices, $i . ':' . ($i + $j) . ':' . $j if $i + $j <= $max;
    last if $i + $j > $max;
  }
}

my @maxs = grep { /:$max:/ and (split /:/)[0] < (split /:/)[2] } @peices;
@peices = grep { ! /:$max:/ } @peices;

foreach (@maxs) {
  /^(\d+):\d+:(\d+)$/;
  my @work = grep { ! /:$1:/ and ! /^$1:/ and ! /:$2:/ and ! /:$2$/ } @pieces;
  tail($_, @work);
}

sub tail {
  my ($chain, @list) = @_;
  head($chain, @list);
  my ($matubi) = $chain =~ /:(\d+)$/;
  foreach my $item (grep /^$matubi:/, @list) {
    my $tmp = $chain;
    $tmp =~ s/\d+$//; $tmp .= $item;
    if (($tmp =~ tr/://) == $max - 1) {
      $tmp =~ s/:/_/g;
      print "$tmp\n";
      $count++;
    } else {
      $item =~ /^(\d+):(\d+):(\d+)$/;
      my @work = grep { ! /\b$1\b/ and ! /\b$2\b/ and  ! /:$3:/ and ! /:$3$/} @list;
      $tmp =~ /^(\d+):.*:(\d+)$/;
      @work = grep { ! /^$2:\d+:$1$/ } @work;
      tail($tmp, @work);
    }
  }
}

sub head {
  my ($chain, @list) = @_;
  my ($atama) = $chain =~ /^(\d+):/;
  foreach my $item (grep /:$atama$/, @list) {
    my $tmp = $chain;
    $tmp =~ s/^\d+//; $tmp = $item . $tmp;
    if (($tmp =~ tr/://) == $max - 1) {
      $tmp =~ s/:/_/g;
      print "$tmp\n";
      $count++;
    } else {
      $item =~ /^(\d+):(\d+):(\d+)$/;
      my @work = grep { ! /\b$2\b/ and ! /\b$3\b/ and ! /:$1:/ and ! /^$1:/ } @list;
      $tmp =~ /^(\d+):.*:(\d+)$/;
      @work = grep { ! /^$2:\d+:$1$/ } @work;
      head($tmp, @work);
    }
  }
}

print "解の数: $count\n";

プログラムの解説

今回のパズルを解くために、少し作戦を立ててみました。正解を組み立てるために、まず最初に小さな部品を作ります。部品は、３つの数字を繋いだ 1:3:2 のような形になります。中央の値は、両隣の数字の和になっています。この部品は２つの円に置くことができ、円の重なったところに中央の値が入ります。このような部品を、２つの数字の順列を生成しながら、最大値を超えないものすべてを作ります。そして、中央が最大値なっている部品 (最大値は必ず中央になる) を最初に配置して、その両端に繋げることのできる部品を繋ぎ、最終的に解を得ます。部品は、配列 @pieces に格納しておきます。円が５つ (1 から 9) の場合の @pieces の内容は、次のようになります。

最初に配置できるのは、中央が最大値 9 になっている部品 1:9:8, 2:9:7, 3:9:6, 4:9:5 の４つです (逆順値の部品 8:9:1, 7:9:2, 6:9:3, 5:9:4 は、重複解となるので最初から排除しておきます)。この４つの部品を foreach ループを使って、１つずつ再帰型サブルーチンを使って探索していくことになります。呼び出しおよびサブルーチンのループでは、現時点で使用不可能な部品を除いた部品 (繋げることができる部品ではない) を引数として渡します。例えば 3:9:6 で探索を始めた場合には、部品の分類は以下のようになります。

tail の呼び出しおよび tail と head のループでは、１の "使用不可の部品" と２の "繋ぐことができない部品" を除外して、３の "繋ぐことのできる部品" と４の "未使用の数字のみで構成される部品" を引数として渡します。ただこれのみで繋いでいったのでは、充分ではありません。最初の呼び出しでは現れないのですが、ループの途中で出現してしまいます。例えば、3:9:6 に 6:8:2 を繋いで 3:9:6:8:2 を作った場合に、"繋ぐことができる部品" として 2:5:3 が残ってしまいます (実際には、前後どちらに繋いでも数字が重複してしまうため駄目なのですが)。これをチェックするために、次のコードを入れています。

解を生成する探索は、tail と head の２つの再帰型サブルーチンを使います。tail は末尾に部品を繋ぎ、head は頭に部品を繋ぐ役割をします。tail で末尾に繋ぐことのできるパターンをすべて生成して、tail だけで完成した解を除いて残りのすべてを head に渡します。こうすることで、すべての解を得ることができます。tail と head の２つのサブルーチンは、正規表現さえ理解できれば易しいと思います。

今回のプログラムでは、部品の接続文字として : (コロン) を使って、表示の際に _ (アンダースコア) に変換しています。それでは、最初から _ にした方が良いと思うかも知れません。しかし _ は単語構成文字に含まれるために、変数名や正規表現により神経を使わなければならなくなります。例えば、変数名の $matubi: は、${matubi}_ のように書かなければなりません。また次の正規表現は、下の行のように書く必要があります。

部品の各々の数字を捕捉したい場合に、\b だけを使ってマッチさせると 3_9_6 では単語境界が先頭と末尾だけになるので失敗します。: を使った 3:9:6 では、先頭と末尾と共に数字と : の接した位置も単語境界になります。また、正規表現で選択を使うと、処理時間がより掛かるようになります。下の実行結果の $max = 19 の実行時間は 72 秒ですが、選択を使ったプログラムでは : から _ に変換する処理がないにもかかわらず 10 秒くらい多く掛かります。

プログラムを実行した結果は、以下のようになります。実行時間は、例によって私の速くないパソコンでの結果です。

今回のプログラムは、内容がほぼ同じのサブルーチンが並んでいて、いかにも素人っぽく (まあ紛れもない素人だが) なってしまいました。最初に作ったプログラムの骨組みは、次のようになっていました。

この最初のプログラムを実行すると、頭に繋げる部品と末尾に繋げる部品を foreach の平坦なリストで扱っているために、同一解が発生してしまいます。例えば 3:9:6 の頭に 1:4:3 を繋ぎ、末尾に 6:8:2 を繋いで 1:4:3:9:6:8:2 を生成する順序は、どちらを先にするかによって２つあります。１つの再帰型サブルーチンの中では、この繋ぐ順序の制御が非常に難しく今回は諦めました。そのうちいいアイデアが浮かんだら、直すことにしましょう。